КС-грамматика определяет структуру цепочек и
позволяет строить цепочки определенного языка. Магазинные автоматы, подобно
рассмотренным ранее конечным автоматам, позволяют решать для контекстно-свободных
языков задачу распознавания, которая заключается в том, что по заданной
цепочке необходимо определить принадлежит ли она заданному языку.
В работах, связанных с формальными языками и грамматиками, используется модель магазинного автомата,
состоящая из входной ленты, устройства управления
и вспомогательной ленты, называемой магазином или стеком.
Входная лента
разделяется на клетки (позиции) , в каждой из которых может быть
записан символ входного алфавита. При этом предполагается, что в
неиспользуемых клетках входной ленты расположены пустые символы e.
Вспомогательная лента также разделена на клетки, в которых могут
располагаться символы магазинного алфавита. Начало вспомогательной ленты
называется дном магазина.
Связь устройства управления с лентами осуществляется двумя головками, которые
могут перемещаться вдоль лент.
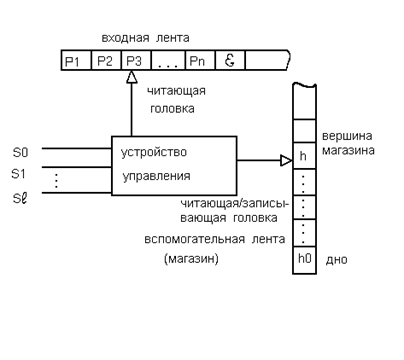
Рис. 3.1. Модель магазинного автомата
Головка входной ленты может перемещаться только в
одну сторону - вправо или
оставаться на месте. Она может выполнять только чтение. Головка
вспомогательной ленты способна выполнять как чтение, так и запись, но эти
операции связаны с перемещением головки определенным образом:
- при записи головка предварительно сдвигается на одну позицию вверх, а
затем символ заносится на ленту,
- при чтении символ, находящийся под головкой считывается с ленты, а
затем головка сдвигается на одну позицию вниз,т.о.головка всегда
установлена против последнего записанного символа. Позицию, находящуюся в
рассматриваемый момент времени под головкой, называют вершиной магазина.
|
Определение.Магазинный автомат М определяется следующей совокупностью семи объектов: M={P , S , sо , f , F , H , hо }, |
где
P - входной алфавит,
S - алфавит состояний,
sо - начальное состояние,
sо Î S ,
F - множество конечных состояний ,F является подмножеством S,
H - алфавит
магазинных символов, записываемых на вспомогательную ленту,
hо- маркер дна, он всегда записывается на дно магазина , hо Î H,
f - функция переходов
f : {P È {e }} x S x H ® S x H*
,
если М-автомат -
детерминированный, и
f:{P È {e }} x S x H ® M(S x
H*) ,
если М-автомат -
недетерминированный.
Функция f отображает тройки ( pi , sj ,
hk ) в пары ( sr , u
) , где u Î H*
и hk - символ в вершине магазина, для детерминированного
автомата или в множество пар для недетерминированного автомата.
Эта функция описывает изменение состояния магазинного автомата, происходящее
при чтении символа с входной ленты и премещении входной головки.
В дальнейшем при построении магазинных автоматов потребуются две разновидности
функций переходов, изменяющих состояние автомата без перемещения входной
головки: 1) функция переходов с пустым символом в качестве входного символа:
f0( s, e, h) = ( s', b),
которая,
независимо от того какой символ находится под читаюшей гловкой входной ленты,
предписывает прочитать символ h из вершины магазина, изменить состояние автомата на s' и записать
цепочку b в
магазин.
2)функция переходов с определенным входным символом:
f*( s, a, h) = ( s', b),
которая предписывает изменение состояния и запись цепочки в магазин при условии, что символ a читается входной головкой, а в вершине магазина находится символ h .
Работа магазинного автомата.
Чтобы описать как работает автомат, введем понятие конфигурации.
|
Определение. Конфигурацией автомата М называют тройку (s, a , g ) Î S x P* x H* , |
где s - текущее состояние
управляющего устройства,
a
-неиспользованная часть входной цепочки a Î P* ,самый левый символ этой
цепочки a находится под головкой.
Если a =e , то считается, что входная цепочка
прочитана.
g -цепочка , записанная
в магазине, g Î
H* ,самый правый символ цепочки считается вершиной магазина. Если g=
$ , то магазин пуст.
Работа автомата может быть представлена как смена конфигураций. Один такт
работы автомата заключается в определении новой конфигурации по заданной. Это
записывается так:
( s, aa , g h ) |-- ( s', a ,
gb )
При этом предполагается, что автомат читает символ a, находящийся под головкой, и символ h,
находящийся в вершине магазина, определяет новое состояние s' и записывает цепочку b в
магазин вместо символа h. Если b
=$ , то верхний символ оказывается удаленным из магазина.
Такая смена конфигураций возможна, если функция f(
s, a, h ) определена и ей принадлежит
значение ( s', b ).
Описанный такт работы выполняется с перемещением головки. Для описания работы
автомата нам потребуется другой вид такта, предполагающий изменение состояний и
магазина без перемещения входной головки. Если f0(s, e, h) определена и
ей принадлежит значение (s', b )
, то он определяет смену конфигураций так:
( s, aa , g h ) |-- ( s', aa , gb )
Таким образом, могут быть три случая при работе автомата:
- f(s, a, h) определена и выполняется такт работы,
- f(s, a, h) не определена, но определена функция f0(s, e, h) и выполняется пустой такт.
- Функции f(s, a, h) и f0(s, e, h) не определены, в этом случае дальнейшая работа автомата невозможна.
В общем виде действия, задаваемые функцией переходов и
выполняемые автоматом, демонстрирует следующая форма записи:
f(s, <входной символ>, <магазинный символ>)=(s1, <заносимая цепочка>)
При этом следует иметь в виду, что при выполнении такта
вначале читается символ в вершине, а затем на его место заносится новый символ
или цепочка. Отдельные значения функции переходов часто называют
командами магазинного автомата.
Начальной
конфигурацией называется конфигурация (sо,
a , hо) ,
где sо -начальное
состояние и hо - маркер
дна магазина, а заключительной - конфигурация
(s, $ , $) , где s принадлежит множеству конечных состояний F.
Для обозначения последовательности сменяющих друг друга конфигураций условимся
использовать знак |--*. Таким образом последовательность
( s1, a 1, g 1 ) |-- ( s2, a 2, g 2) |-- ...|-- ( sn, a n,g n )
записывается в сокращенном виде так:
(s1,a 1, g 1 ) |--* ( sn, a n,g n ).
Язык, допускаемый магазинным автоматом.
|
Определение. Цепочка a называется допустимой для автомата М, если существует последовательность конфигураций, в которой первая конфигурация является начальной c цепочкой a , а последняя - заключительной. (sо, a, hо) |--* (s1, $ , $) , где s1 Î F . |
|
Определение.Множество цепочек, допускаемых автоматом М, называется языком, допускаемым или определяемым автоматом М, и обозначается L(М). |
L(М)= {a ¦ ( sо, a, hо ) ¦--* ( s', $, $) & s' Î F }
Чтобы лучше представить себе
работу магазинного автомата, рассмотрим два примера. Пусть задан магазинный
автомат М1 в следующем виде:
М1: P = {a , b}; S = {s0 , s1 , s2}; H = {h0 , a}; F = {s0};
f (s0 , a , h0)
= (s1 , h0a),
f (s1 , a , a) = (s1 , aa),
f (s1 , b , a) = (s2 , $),
f (s2 , b , a) = (s2 , $),
f (s2 , e , h0) = (s0 ,
$).
Этот автомат является детерминированным, поскольку каждому набору аргументов
соответствует единственное значение функции. Работу автомата при распознавании
входной цепочки aabb можно представить в виде последовательности конфигураций:
(s0,aabb,h0)
|-- (s1,abb,h0a) |-- (s1,bb,h0aa)
|-- (s2,b,h0a) |-- (s2,$,h0) |-- (s0,$,$)
.
Нетрудно проверить, что при задании входной
цепочки aabbb автомат не сможет закончить работу. Следовательно эта цепочка не
принадлежит языку, допускаемому автоматом M1.
Магазинный автомат М2, заданный следующим описанием:
М2:
P = {a , b}; S = {s0, s1 , s2}; H = {h0,
a , b}; F = {s2};
(1)f (s0 , a , h0)
= (s0, h0a),
(2)f (s0 , b , h0) = (s0,
h0b),
(3) f (s0 , a , a) = {(s0,aa)
, (s1 , $)},
(4) f (s0 , b , a) = (s0,ab),
(5) f (s0 , a , b) = (s0 , ba),
(6) f (s0 , b , b) = {(s0 ,
bb) , (s1 , $)},
(7) f (s1 , a , a) = (s1, $),
(8) f (s1 , b , b) = (s1, $),
(9) f (s2 , e , h0) = (s2 ,
$),
является недетерминированным
автоматом, поскольку одному и тому же набору аргументов, например (sо ,
a, a), соответствуют два значения функции. Работу автомата рассмотрим для
входной цепочки abba. Если использовать последовательность команд
(1),(4),(6.1),(5), то получим последовательность конфигураций:
(s0,abba,h0) |-- (s0,bba,h0a),
(1)
|-- (s0,ba,h0ab), (4)
|-- (s0,a,h0abb), (6.1)
|-- (s0,$,h0abba). (5),
которая показывает, что дальнейшая работа невозможна, т.к.
входная цепочка прочитана и переход (s0,$,h0abba) не
определен. Если же использовать последовательность команд
(1),(4),(6.2),(3),(9), то получим заключительную конфигурацию:
(s0,abba,h0)
|-- (s0,bba,h0a), (1)
|-- (s0,ba,h0ab), (4)
|-- (s1,a,h0a),
(6.2)
|-- (s1,$,h0),
(3)
|-- (s2,$,$)
. (9).
Т.о. можно сделать вывод о том,
что цепочка abba допускается автоматом М2.
В общем случае справедливо следующее утверждение.
Построение магазинного автомата.
|
Утверждение. Если Г = { Vт , Va , I , R } является КС-грамматикой, то по ней можно построить такой магазинный автомат М, что L(M) = L(Г). |
В основе доказательства лежит способ построения магазинного автомата по заданной
КС-грамматике.Чтобы сделать процесс построения автомата более простым и
наглядным, условимся использовать магазинные автоматы с одним состоянием s0.
Итак, пусть задана грамматика Г = { Vт , Va , I , R }. Определим
компоненты автомата М следующим образом:
S = { s0
}, P = Vт ,
H = VтÈ VaÈ { h0}
, F = { s0 },
в качестве начального состояния автомата примем s0
и построим функцию переходов так:
1. Для всех A Î
VA , таких что встречаются в левой части правил
<A> ® a , построим команды
вида:
f0( s 0 , e , <A> ) = ( s0 , aR ),
где aR -зеркальное отображение a .
2. Для всех a ÎVт построим команды вида
f ( s0 , a , a ) = ( s0 , $ )
3. Для перехода в конечное состояние построим команду
f ( s0 , e , h0 ) = ( s0 , $ )
4. Начальную конфигурацию автомата определим в виде:
( s0 , w , h0<I> ),
где w - заданная цепочка,
записанная на входной ленте.
Автомат, построенный по приведенным выше правилам, работает следующим образом.
Если в вершине магазина находится терминал, и символ, читаемый с входной ленты,
совпадает с ним, то по команде типа (2) терминал удаляется из магазина, а
входная головка сдвигается. Если же в вершине магазина находится нетерминал, то
выполняется команда типа (1), которая вместо терминала записывает в магазин
цепочку, представляющую собой правую часть правила грамматики. Следовательно,
автомат, последовательно заменяя нетерминалы, появляющиеся в вершине магазина,
строит в магазине левый вывод входной цепочки, удаляя полученные терминальные
символы, совпадающие с символами входной цепочки. Это означает, что каждая
цепочка, которая может быть получена с помощью левого вывода в грамматике Г,
допускается построенным автоматом М.
Пример построения автомата.
Процедуру построения автомата рассмотрим на примере грамматики:
Г1. 9: R={<E> ®<E> + <T> | <T>,
<T>
® <T> * <F> | <F>,
<F> ® (
<E> ) | a}.
Для искомого автомата имеем:
M3: P = {a, + , * , ) , ( }, H = {E , T , F , a , + , x , ) , h0 , ( }, S = {s0 }, F = {s0}
Для всех правил грамматики строим команды типа
(1):
(1) f0 (s0 , e , E) = {(s0 , T+E) ;
(s0 , T)},
(2) f0 (s0 , e , T) = {(s0 , F*T) ; (s0
, F)},
(3) f0 (s0 , e , F) = {(s0 , )E( ) ;
(s0 , a)},
Для всех терминальных символов
строим команды типа (2):
(4) f ( s0,
a, a ) = ( s0, $ ),
(5) f ( s0 , + , + ) = (s0
, $ ),
(6) f ( s0 , * , * ) = (s0
, $ ),
(7) f ( s0 , ( , ( ) = (s0
, $ ),
(8) f ( s0 , ) , ) ) = (s0
, $ ),
Для перехода в конечное состояние
построим команду:
(9) f (s0 , e , h0) = ( s0 , $ ).
Построенный автомат является
недетерминированным.
Начальную конфигурацию с цепочкой a + a*a запишем так: (s0 , a+a*a ,
h0E).
Последовательность тактов работы построенного автомата, показывающая, что
заданная цепочка допустима, имеет вид:
(s0 , a+a*a , h0E)
|-- (s0 , a+a*a , h0T+E) |--
(s0 , a+a*a , h0T+T) |-- (s0
, a+a*a , h0T+F) |--
(s0 , a+a*a , h0T+a) |-- (s0
, +a*a , h0T+) |--
(s0 , a*a , h0T) |--
(s0 , a*a , h0F*T) |--
(s0 , a*a , h0F*F)
|-- (s0 , a*a , h0F*a)
|--
(s0 , *a , h0F* ) |--
(s0 , a , h0F) |--
(s0 , a , h0a) |-- (s0
, $ , h0) |--
(s0 , $ , $).
Отметим, что последовательность правил, используемая построенным автоматом, соответствует левому выводу входной цепочки:
E
Þ E+T Þ T+T Þ F+T Þ a+T Þ a+T*F Þ a+F*F Þ a+a*F Þ a+a*a.
Если по такому выводу строить дерево, то построение будет происходить сверху вниз, т.е. от корня дерева к листьям.
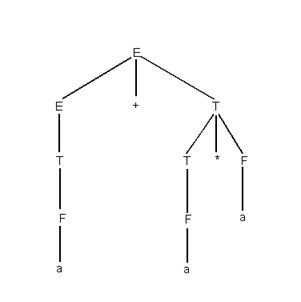
Рис. 3.2. Дерево, соответствующее левому выводу цепочки a+a*a.
.
Такой способ построения дерева по
заданной цепочке называется нисходящим.
Магазинные автоматы называют часто распознавателями, поскольку они определяют,
является ли цепочка, подаваемая на вход автомата, допустимой или нет, и
следовательно, отвечают на вопрос, принадлежит ли эта цепочка языку,
пораждаемому грамматикой, использованной для построения автомата.
Учитывая характер построения вывода в магазине, автоматы рассмотренного типа
называют нисходящими
распознавателями.
Еще раз подчеркнем, что доказательство допустимости цепочки нисходящим
магазинным автоматом (НМА) предусматривает поиск определенной
последовательности конфигураций.
Такой поиск может существенно увеличить время работы автомата.
Детерминированные автоматы не требуют поиска и работают быстрее, поэтому
именно такие автоматы применяются на практике. Детерминированные
автоматы-распознаватели могут быть построены не для всех, а только для
некоторых видов КС-грамматик.
|
Определение. Если язык L допускается детерминированным М-автоматом , то он называется детерминированным языком. |
Учитывая значение детерминированных автоматов для практических
применений, посвятим им последующие разделы.