Пред. страница   . След. страница   Раздел   Содержание

_____________________________________________________________________________

4.6. Минимизация числа состояний А - преобразователей

Задача проектирования автоматов, как и любая другая задача синтеза, является неоднозначной. Это означает, что для одних и тех же исходных данных могут быть получены разные решения, удовлетворяющие условиям задачи. Например, для заданного перевода могут быть построены автоматы, имеющие различное число состояний, или автомат, имеющий избыточные состояния. В большинстве случаев удобнее работать с более компактным описанием устройства, поскольку такое описание является более наглядным, его легче понимать и легче тестировать. Исходя из этого положения, после построения автомата целесообразно проверить наличие в нем избыточных состояний и удалить их.

В разделе 2.5 был рассмотрен способ минимизации числа состояний автоматов без выходов. В настоящем разделе рассматриваются методы минимизации автоматов с выходными преобразователями или выходами. Кроме того, в нем обсуждаются вопросы минимизации не полностью определенных или частичных автоматов, которые часто встречаются в практических приложениях.

4.6.1. Минимизация полностью определенных А - преобразователей

Задачу удаления избыточных состояний, если таковые имеются, можно рассматривать как задачу построения автомата, выполняющего такое же преобразование входных последовательностей, как и исходный автомат, но имеющего меньшее число состояний. Избыточные состояния полностью определенного автомата обычно называют эквивалентными. Точное определение понятия эквивалентности состояний можно сформулировать так.

Определение. Два состояния s_i и s_j автомата А называются эквивалентными, если независимо от того, какое из состояний s_i или s_j принять за начальное, любое входное слово p^~ преобразуется автоматом А в одинаковое выходное слово w^~.

Это определение задает отношение эквивалентности на множестве состояний S автомата, поскольку для каждой пары состояний s_i и s_j можно установить эквивалентные они или нет. Напомним, что отношение эквивалентности, для обозначения которого используется символ «тильда», обладает следующими свойствами:

a) рефлексивности: s_i ~ s_j

b) симметричности: если s_i ~ s_j, то s_j ~ s_i ,

c) транзитивности: если s_i ~ s_j и s_j ~ s_k, то s_i ~ s_k

Отношение эквивалентности разбивает S на непересекающиеся классы эквивалентности, которые обладают следующими свойствами:

a) классы включают состояния, попарно эквивалентные друг другу,

b) множество классов эквивалентности обладает полнотой S=ÈE_k,

c) классы эквивалентности не пересекаются E_k Ç E_l=Æ,

d) классы эквивалентности являются замкнутыми, т.е. под воздействием каждого входного символа автомат переходит в состояние, принадлежащее одному классу

Для иллюстрации понятия эквивалентности рассмотрим несколько простых случаев выявления и преобразования эквивалентных состояний автомата. Так, состояния s_i и s_j фрагмента диаграммы переходов, изображенного на рис. 4.14а, эквивалентны, поскольку под действием одинаковых входных символов из них выполняется переход в одно и то же состояние и при этом вырабатываются одинаковые выходные символы. Эквивалентные состояния s_i и s_j можно заменить одним состоянием s_j, как это показано на рис. 4.14b.

Ситуация, когда из состояний s_i и s_j возможен переход в несколько состояний, показана на рис. 4.14с. В приведенном фрагменте диаграммы переход из состояний s_i и s_j под действием одинаковых входных символов происходит в одно и то же состояние с выработкой одинаковых выходных сигналов. Следовательно, состояния s_i и s_j эквивалентны и их можно объединить в одно состояние, как показано на рис. 4.14d.

Менее очевидна эквивалентность состояний s_i и s_j фрагмента диаграммы переходов, изображенного на рис. 4.14e. Нетрудно, однако, проверить, что при подаче на вход символов p₁ и p₂ выходные последовательности не изменятся, если символы s_i и s_j поменять местами. Неизменность выходных символов при замене состояния s_i на s_j и s_j на s_i говорит о том, что эти состояния эквивалентны, и их можно заменить одним состоянием, как это показано на рис. 4.14f.

a)

b)

c)

d)

e)

f)

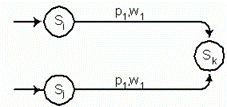
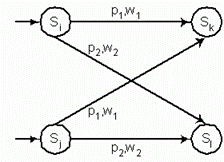
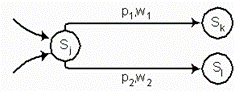
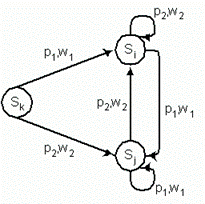
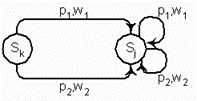
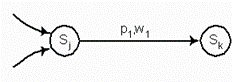Рис. 4.14 Фрагменты диаграмм переходов, иллюстрирующие простые случаи эквивалентности состояний s_i и s_j – a,c,e и фрагменты диаграмм после объединения этих состояний – b,d,f.

В общем случае, условия, позволяющие сделать вывод об эквивалентности двух состояний автомата, могут быть сформулированы следующим образом:

1. для любых входных символов p_k єP выходные символы, вырабатываемые автоматом, должны совпадать,
2. для любых входных символов p_k єP переходы из состояния s_i в состояние s_j должны происходить либо в одно и то же состояние, либо в эквивалентные состояния

Выявление эквивалентных состояний является только одним из шагов процедуры построения автомата с минимальным числом состояний, который позволяет найти классы эквивалентности. Для выявления эквивалентных состояний используют таблицу специального вида – треугольную таблицу. Полную процедуру построения автомата можно разделить на 5 шагов:

1. построение треугольной таблицы,
2. заполнение треугольной таблицы,
3. уточнение разметки треугольной таблицы,
4. построение классов эквивалентности,
5. построение таблицы переходов искомого автомата.

Чтобы сделать процедуру более наглядной, совместим описание ее шагов с построением минимального автомата для автомата А, заданного таблицей 4.5.

Первый шаг процедуры предусматривает построение треугольной таблицы без диагональных элементов.

Если заданный автомат имеет n состояний, то столбцы таблицы нумеруются слева направо 0,1,…, n-2, а строки сверху вниз 1,2,…, n-1. Таким образом, каждой паре состояний с индексами I и j в таблице соответствует одна клетка.

Второй шаг процедуры заключается в заполнении таблицы. Этот шаг выполняется путем последовательного просмотра всех пар состояний в таблице переходов и выходов автомата, проверке выполнения условий эквивалентности и занесении символов результатов проверки в соответствующую клетку треугольной таблицы. Символы результатов проверки определяются по следующим правилам:

a) если для состояний s_i и s_j не выполняется первое условие эквивалентности, то в клетку, соответствующую индексам i и j, заносится крестик, что означает неэквивалентность этих состояний,

b) если для состояний s_i и s_j выполняются первое и второе условия эквивалентности, то в клетку, соответствующую индексам i и j, заносится символ тильда, что означает эквивалентность этих состояний,

c) если для состояний s_i и s_j выполняется первое условие эквивалентности и не выполняется второе, то в клетку, соответствующую индексам i и j, заносятся индексы тех состояний, от которых зависит эквивалентность рассматриваемой пары s_i и s_j.

Таблица 4.5. Таблица переходов и выходов автомата А.

	P0	P1
s0	s1, w0	s2, w0
s1	s4, w0	s5, w0
s2	s3, w1	s4, w1
s3	s0, w1	s2, w1
s4	s4, w0	s5, w0
s5	s3, w1	s4, w1

1	1,4 2,5
2	X	X
3	X	X	0,3 2,4
4	1,4 2,5	~	X	X
5	X	X	~	0,3 2,4	X
	0	1	2	3	4

Рис. 4.15 Заполненная треугольная таблица автомата А.

1	1,4 2,5
2	X	X
3	X	X	X
4	1,4 2,5	~	X	X
5	X	X	~	X	X
	0	1	2	3	4

Рис 4.16. Треугольная таблица автомата после разметки.

В таблице переходов рассматриваемого автомата для пар состояний (s₀,s₂), (s₁,s₂),

(s₀,s₃), (s₁,s₃) , например, не выполняется первое условие эквивалентности, поэтому в соответствующие клетки треугольной таблицы нужно поместить крестики. Для пар состояний (s₁,s₄) и (s₂,s₅) выполняются оба условия эквивалентности, поэтому в клетки таблицы с номерами 1, 4 и 2, 5 нужно занести значки тильды. Об эквивалентности состояний (s₂,s₃) и (s₃,s₅), для которых выполняется первое условие и не выполняется второе, заранее ничего сказать нельзя, поскольку их эквивалентность зависит от эквивалентности состояний (s₀,s₃) и (s₂,s₄). В клетки треугольной таблицы. соответствующие рассматриваемым состояниям , нужно записать индексы тех состояний, от которых зависит их эквивалентность. После просмотра всех пар состояний получим треугольную таблицу, изображенную на рис. 4.16

На третьем шаге процедуры построения выполняется уточнение разметки, которое заключается в последовательном просмотре пар номеров состояний, записанных в клетки треугольной таблицы, для проверки их эквивалентности. Если в рассматриваемой клетке таблицы расположены индексы i и j, и если обнаруживается, что в клетке таблицы, соответствующей этим индексам, находится крестик, то в рассматриваемую клетку вместо индексов i и j нужно также поместить крестик. Такой просмотр может повторяться несколько раз до тех пор, пока не будет получена треугольная таблица, в которой нельзя более отметить крестиком ни одной клетки. В нашем примере клетки треугольной таблицы с номерами 2,3 и 3,5 содержат индексы состояний 0,3 и 2,4, от которых зависит эквивалентность рассматриваемых пар. Однако, состояния 0,3 и 2,4 неэквивалентны, поскольку соответствующие им клетки треугольной таблицы отмечены крестиками. Следовательно, состояния с индексами 2,3 и 3,5 не могут быть эквивалентными, и в соответствующие им клетки надо занести крестики. В отличие от рассмотренного случая, клетки таблицы с номерами 0,1 и 0,4 содержат индексы состояний 1,4 и 2,5, которые являются эквивалентными. Следовательно, состояния 0,1 и 0,4 также являются эквивалентными. Вид таблицы, полученной после уточнения разметки, показан на рис. 4.17

Четвертый шаг процедуры состоит в том, что из треугольной таблицы выписываются все пары эквивалентных состояний, и группы попарно эквивалентных состояний объединяются в классы эквивалентности.

Для рассматриваемого примера имеем четыре пары эквивалентных состояний, из которых получаем следующие классы эквивалентности:

(s₀, s₁, s₄), (s₂, s₅, (s₃).

Последний шаг процедуры предполагает построение таблицы переходов и выходов искомого автомата с минимальным числом состояний. Для этого каждый класс эквивалентности примем в качестве нового состояния искомого автомата и введем новые обозначения для новых состояний. В нашем примере это будут состояния s₀^’, s₁^’, s₂^’

~
X	X
X	X	X
~	~	X	X
X	X	~	X	X

Рис 4.17.. Треугольная таблица автомата после уточнения.

Таблица 4.6. Таблица переходов и выходов автомата с минимальным числом состояний.

	P0	P1
s0^’	s0^’, w1	s1^’, w0
s1^’	s2^’, w0	s0^’, w1
s2^’	s0^’, w0	s1^’, w1

Затем в таблице переходов заданного автомата заменим символ каждого состояния s_i символом того класса эквивалентности, в который входит s_i. После объединения одинаковых строк в таблице переходов и выходов получим таблицу автомата с минимальным числом состояний. Для рассматриваемого примера результатом построения является таблица 4.6.

4.6.2. Минимизация частичных А - преобразователей.

Автоматы являются моделями цифровых устройств, условия работы которых полностью определены. Неопределенности в условиях работы могут возникать из-за того, что некоторые последовательности входных символов никогда не будут подаваться на входы устройства. Это приводить к тому, что некоторые комбинации (s_i, p_k) никогда не появятся при работе автомата. Автоматы, условия работы которых не полностью определены, называются не полностью определенными или частичными автоматами. Для таких автоматов множество определенных и допустимых входных последовательностей обычно является заданным.

Определение. Частичным автоматом называют автомат, у которого функция переходов или функция выходов или обе эти функции определены не для всех пар значений аргументов (s_i, p_k).

Для задания частичных автоматов используются такие же таблицы и диаграммы переходов как и для полностью определенных автоматов. Единственным отличием при задании частичных автоматов является то, что для обозначения неопределенных значений функций переходов и выходов используется прочерк.

Допущение о том, что значения функции выходов могут быть не определены, позволяет сделать вывод о том, что выходные последовательности частичного автомата могут содержать неопределенные символы. Например, выходная последовательность может иметь вид: w₁_ w₂ w₃_ w₄. В этой последовательности символы, стоящие на второй и пятой позициях, являются неопределенными.

Для того, чтобы сравнивать реакции частичного автомата на допустимые входные последовательности вводят понятие непротиворечивых выходных последовательностей.

Определение. Две выходные последовательности называют непротиворечивыми, если в каждой позиции, где символы первой и второй последовательностей определены, эти символы являются одинаковыми.

Например, последовательности a = w₁_ _ w₂ _ w₁ и a^’ = w₁_ w₃ w₂ _ w₁ являются непротиворечивыми, а последовательности a = w₁_ _ w₂ _ w₁ и a^’ = w₁_ _w₃ _ w₁ нет.

Способ минимизации числа состояний частичных автоматов основан на приеме, подобном тому, который был использован при минимизации полностью определенных автоматов. Он заключается в выделении группы состояний, которые в дальнейшем можно заменить одним состоянием. Такие группы называют классами совместимости. Для того, чтобы находить классы совместимости, на множестве состояний автомата задают отношение совместимости.

Определение. Два состояния частичного автомата s_i и s_j называются совместимыми, если при подаче на вход любого допустимого входного слова, независимо от того, какое из состояний s_i или s_j выбирается в качестве начального, на выходе автомата вырабатываются непротиворечивые выходные последовательности.

Отношение совместимости, которое будем обозначать двумя знаками тильда, обладает свойством рефлексивности: s_i ≈ s_j и свойством симметричности: если s_i ≈ s_j , то и s_j ≈ s_i, но не обладает свойством транзитивности.

Условия, позволяющие выявлять совместимые состояния, могут быть сформулированы следующим образом:

1. Значения функций выходов состояний s_i и s_j для всех входных символов должны либо совпадать, либо одно или оба значения должны быть неопределенными,

2. Переходы из состояний s_i и s_j для всех входных символов должны происходить в одно и то же состояние или в совместимые состояния.

Отношение совместимости разбивает множество состояний автомата S на множество классов совместимости

C = {c₁, С₂, …, С_n}.

Особенностью такого разбиения является то. Что классы совместимости могут содержать одинаковые состояния. То есть пересечение классов может быть не пусто c_i ∩ С_j, ≠ 0.

Целью процедуры минимизации является построение автомата с меньшим числом состояний, но выполняющего такое же преобразование, что и исходный частичный автомат. Такой автомат называют совместимым с исходным автоматом, если он удовлетворяет следующему определению.

Определение. Два частичных автомата А и А’ называются совместимыми, если они имеют одинаковое множество допустимых входных последовательностей, и если каждое допустимое входное слово автоматы А и А’ перерабатывают в непротиворечивые выходные слова при условии. Что оба эти автомата находились в начальных состояниях перед подачей входной последовательности.

Для того, чтобы построить автомат, совместимый с заданным, множество классов совместимости должно обладать свойством полноты и замкнутости.

Определение. Множество классов совместимости С называют полным, если каждое состояние из множества S входит хотя бы в один класс совместимости.

Для определения свойства замкнутости классов совместимости необходимо определить сначала отношение следования классов.

Определение. Множество состояний T_kⁱ , в которые переходит автомат из состояний класса совместимости С_k под воздействием входного символа p_i , называют множеством, следующим за С_k.

Определение. Множество классов совместимости С называется замкнутым, если для любого входящего в него класса совместимости множество состояний, следующих за этим множеством, содержится хотя бы в одном классе совместимости множества С.

Приведенные определения позволяют сформулировать утверждение, уточняющее процедуру построения частичного автомата с меньшим числом состояний.

Утверждение. Для того, чтобы автомат, построенный на основе множества классов совместимости, был совместимым с заданным автоматом, множество классов совместимости должно быть полным и замкнутым.

Процедуру построения частичного автомата с меньшим числом состояний можно разделить на следующую последовательность шагов:

1. Построение и заполнение треугольной таблицы,

2. Уточнение разметки треугольной таблицы,

3. Построение максимальных классов совместимости,

4. Построение минимального покрытия,

5. Проверка замкнутости покрытия и возможности удаления избыточных состояний,

6. Построение таблицы переходов искомого автомата.

Как и в предыдущем разделе совместим описание отдельных шагов процедуры с выполнением примера построения автомата, функции переходов и выходов которого приведены в табл. 4.7.

Первый шаг процедуры заключается в построении треугольной таблицы и выявлении совместимых состояний. Треугольная таблица строится так же как и в случае выявления эквивалентных состояний, но заполняется с учетом условий совместимости. Последовательно просматривая все пары состояний заданного автомата, находим, что состояния s₀ и s₂ являются совместимыми, состояния s₀ и s₃ являются несовместимыми, а совместимость остальных состояний остается пока неопределенной. Заполненная треугольная таблица изображена на рис.4.18.

Таблица 4.7. Таблица переходов и выходов автомата.

	a	b	c	d
s0	-	-	s4,1	-
s1	-	s4,1	s3,-	-
s2	s2,0	s1,1	-	s0,0
s3	s2,0	s0,1	s3,0	-
s4	s3,0	-	s2,-	s3,0

1	3,4
2	~	1,4
3	X	0,4	0,1
4	2,4	2,3	2,3 0,3	2,3
	0	1	2	3

Рис. 4.18. Заполненная треугольная таблица автомата А.

На втором шаге процедуры выполняется уточнение разметки треугольной таблицы. Просматривая номера состояний, записанные в клетках таблицы, находим, что совместимость состояний s₂ и s₃ зависит от состояний s₀ и s₁, клетка которых отмечена крестиком. Это означает, что s₂ и s₃ являются несовместимыми состояниями, и в клетку таблицы, соответствующую этим состояниям, нужно занести крестик. Просматривая треугольную таблицу повторно, обнаруживаем, что совместимость состояний s₀ и s₄ зависит от состояний s₂ и s₄, которые отмечены в таблице как совместимые состояния. Следовательно, в клетку, соответствующую паре (s₀,s₄₎, нужно поместить крестик. При последующем просмотре найти несовместимые состояния не удается. Полученная треугольная таблица изображена на рис.4.19.

1	3,4
2	~	1,4
3	X	X	0,1
4	X	2,3	X	2,3
	0	1	2	3

Рис. 4.19. Треугольная таблица автомата А после уточнения..

В этой таблице все пары состояний являются совместимыми, поэтому перейдем к следующему шагу процедуры, который предусматривает построение максимальных классов совместимости.

Опредлениее. Класс совместимости называется максимальным, если он не содержится ни в каком другом классе совместимости.

Для нахождения максимальных классов совместимости нужно построить вначале все классы совместимости, а затем выбрать те классы, которые не являются частью других классов. Вспомним, что отношение совместимости не обладает транзитивностью, поэтому для построения всех классов совместимости воспользуемся следующим приемом. В качестве исходного множества классов совместимости примем множество состояний автомата. Затем из треугольной таблицы будем последовательно выбирать состояние автомата и множество несовместимых с ним состояний. Если в треугольной таблице имеются k столбцов с клетками, отмеченными крестиками, то такой выбор придется повторить k раз. Допустим, что выбран столбец, соответствующий состоянию s’. Выпишем все состояния, отмеченные крестиками в этом столбце, то есть состояния, несовместимые с s’.Затем каждый класс совместимости, полученный на предыдущей итерации, разобьем на два класса. В один класс включим выбранное состояние и все состояния кроме несовместимых с ним. В другой класс включим все состояния, несовместимые с выбранным, и и все состояния за исключением выбранного состояния.

Для рассматриваемого примера вначале выберем состояние s₀. По треугольной таблице определим, что оно несовместимо с состояниями s₃ и s₄. Исходный класс совместимости, совпадающий с множеством состояний автомата, разобьем на два подмножества. Одно подмножество не должно содержать состояние s₀, а другое не должно содержать состояний, несовместимых с s₀. Процесс последовательного построения классов совместимости можно представить в виде диаграммы, изображенной на рис.4,20. Первый ярус этой диаграммы образует множество состояний автомата. На втором ярусе расположены два множества состояний, полученные разделением состояния s₀ и несовместимых с ним состояний s₃ и s₄. Для построения третьего яруса диаграммы выберем состояние s₁ и по треугольной таблице найдем, что оно несовместимо с состоянием s₃. Разбивая множество состояний, содержащих s₁ и s₃ на два подмножества, получаем третий ярус диаграммы. Последний (четвертый) ярус диаграммы строится для состояния s₂, которое является несовместимым с состоянием s₄. После разделения классов, содержащих s₂ и s₄, получаем пять классов совместимости.

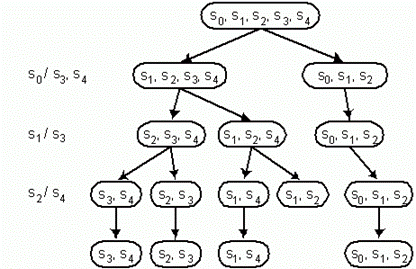
рис. 4.20. Диаграмма построения максимальных классов совместимости.

Класс (s₁, s₂) из полученной совокупности целиком содержится в классе (s₀, s₁, s₂). Следовательно, этот класс не является максимальным классом. После его удаления из полученной совокупности классов в ней останутся только максимальные классы совместимости, которые обозначим следующим образом:

c₁ = (s₀, s₁, s₂), c₂ = (s₁, s₄), c₃ = (s₂, s₃), c₄ = (s₃, s₄).

В построенной совокупности состояния s₁, s₂, s₃, s₄ повторяются в разных классах, поэтому можно предположить, что такая совокупность классов является избыточной, и попытаться найти совокупность классов, обладающую свойством полноты и содержащую наименьшее число классов.

Задача построения такой совокупности классов решается на четвертом шаге процедуры построения частичного автомата с меньшим числом состояний с помощью построения таблицы покрытий.

При построении таблицы покрытий ее столбцы обозначаются состояниями заданного автомата, а строки – классами совместимости. Если состояние s’, расположенное в заголдовке столбца с номером i, входит в класс совместимости c’, расположенный в строке с номером j, то в клетке таблицы с координатами (i,j) помещают галочку. В этом случае говорят, что класс c’ покрывает состояние s’. Для рассматриваемого примера таблица покрытий может быть представлена в виде табл. 4.8.

Таблица 4.8. Таблица покрытий состояний автомата А.

	s0	s1	s2	s3	s4
(s0,s1,s2)	Ú	Ú	Ú
(s1,s4)		Ú			Ú
(s2,s3)			Ú	Ú
(s3,s4)				Ú	Ú

Задача построения совокупности с минимальным числом классов совместимости при работе с таблицей покрытий может быть сформулирована так. Требуется найти минимальную совокупность строк, имеющих отметки в каждом столбце. Совокупность классов, расположенных в заголовках таких строк, называют минимальным покрытием. Для таблицы 4.5.2. минимальное покрытие включает два класса совместимости:

c_min = {(s₀,s₁,s₂)}, (s₃,s₄)}.

Полученная совокупность классов является полной и не содержит повторяющихся состояний. Однако, нам неизвестно, является ли эта совокупность замкнутой. Проверке замкнутости и построению покрытия, обладающего свойством замкнутости, посвящен пятый шаг процедуры построения частичного автомата.

Для проверки замкнутости построенной совокупности классов совместимости необходимо построить для каждого класса множество следующих за ним состояний для каждого входного символа. Если каждое множество, следующее за рассматриваемым классом совместимости, не содержится в заданной совокупности классов, то к заданной совокупности нужно добавить класс совместимости, содержащий это следующее множество. Таким образом, число классов совместимости в заданной совокупности может увеличиться. Увеличениеи числа классов в совокупности, в свою очередь, приводит к появлению состояний, повторяющихся в разных классах. В некоторых случаях повторяющиеся состояния можно удалить, если они не нарушают свойство замкнутости.

Если для заданного автомата по таблице 4.5.1. построить множества, следующие за классами совместимости c₁ и с₄ совокупности c_min, то получим следующий результат:

T₁^a = (s₂), T₁^b = (s₁, s₄), T₁^c = (s₃, s₄), T₁^d = (s₀),

T₄^a = (s₂,s₃), T₄^b = (s₀), T₄^c = (s₂,s₃), T₄^d = (s₃).

Проверяя вхождение полученных множеств в классы совокупности c_min, находим, что множества T₁^b = (s₁, s₄) и T₄^c = (s₂,s₃) не входят в классы совокупности c_min. Это означает, что необходимо добавить эти классы к совокупности c_min. В результате получим полную и замкнутую совокупность классов в виде:

c’ = {(s₀,s₁,s₂), (s₃,s₄), (s₁,s₄), (s₂,s₃)}.

Таким образом, наша попытка использования минимального покрытия оказалась неудачной, что случается, конечно, не всегда.

Попытаемся исключить в покрытии c’ повторяющиеся состояния. Рассмотрим, например, состояние s₂, которое входит в два класса совместимости. Если исключить это состояние из класса (s₀, s₁, s₂), то изменится множество состояний , следующих за этим классом T₁^b = (s₄), и класс (s₁, s₄) окажется замкнутым. После исключения класса (s₁, s₄) из c’, получим:

c” = {(s₀, s₁), (s₃, s₄), (s₂, s₃)}.

В этой совокупности состояние s₃ повторяется дважды, но исключение его из любого класса приводит к нарушению свойства замкнутости. Таким образом, совокупность c” являтся минимальной полной совокупностью классов совместимости, обладающей свойством замкнутости.

Последний - шестой шаг процедуры построения автомата предусматривает построение таблицы переходов для найденного покрытия c”.

Чтобы построить таблицу переходов искомого автомата, сопоставим каждому классу найденного минимального покрытия c” новый символ состояния. Так, в нашем примере сопоставим классам совместимости совокупности c” : c₁ = (s₀, s₁), c₃ = (s₂, s₃), c₄ = (s₃, s₄) символы новых состояний s₀’, s₁’, s₂’. Затем в исходной таблице переходов и выходов заданного автомата заменим символы состояний новыми символами. Если состояния исходного автомата входят в несколько классов совместимости, то такую замену можно выполнить несколькими способами. Например, состояние s₃ в исходной таблице можно заменить новым состоянием s₁’ или s₂’, поскольку s₃ входит в класс c₃ и в класс c₄. Допустим, что состояние s₃ заменяется на s₂’. В этом случае получаем таблицу переходов4.9.

Таблица 4.9. Таблица переходов автомата А после замены состояний.

	a	b	c	d
s0’	-	-	s2’,1	-
s0’	-	s2’,1	s2’,-	-
s1’	s1’,0	s0’,1	-	s0’,0
s2’	s1’,0	s0’,1	s1’,0	-
s2’	s1’,0	-	s1’,-	s1’,0

При заполнении клеток этой таблицы опять прходится выбирать, каким новым символом заменить старый символ. Такой выбор нужно выполнять так, чтобы не нарушались свойства замкнутости используемого покрытия. В рассматриваемом примере состояние s₃, расположенное в строке s₁ и столбце с исходной таблицы, следует заменить на состояние s₂’, поскольку множество состояний T₁^c = (s₃, s₄), следующих за s₀’, соответствует новому состоянию s₂’. В то время как, состояние s₃, расположенное в строке s₃ и столбце с исходной таблицы, следует заменить на состояние s₁’, поскольку множество состояний T₃^c = (s₂, s₃), следующих за состоянием s₂’, соответствует новому состоянию s₁’.

После замены всех старых символов состояния новыми получаем таблицу, строки которой можно объединить. Если при объединении клеток двух строк, расположенных в одном столбце, имеет место ситуация, когда один из выходных символов определен, а другой нет, то после объединения строк в эту клетку нужно записать определенный выходной символ.

В результате такого объединения строк заданный частичный автомат может превратиться в полностью определенный автомат. Таблица переходов искомого автомата, полученная после объединения строк таблицы 4.9., представлена в таблице 4.10.

Таблица 4.10. Таблица переходов и выходов автомата А после минимизации.

	a	b	c	d
s0’	-	s2’,1	s2’,1	-
s2’	s1’,0	s1’,0	-	s0’,0
s3’	s1’,0	s0’,0	s1’,0	s1’,0

Эта таблица описывает полностью определенный автомат, поскольку при объединении строк с состояниями s₀’ и s₂’ в столбце, отмеченном входным символом c , объединились переходы, для одного из которых выходной символ был определен.

____________________________________________________________

Пред. страница   . След. страница   Раздел   Содержание