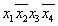 и
и 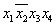 , то, вынеся за скобки общий множитель, получаем:
, то, вынеся за скобки общий множитель, получаем: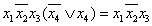
8.3. МИНИМАЛЬНЫЕ ФОРМЫ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ
8.3.1. Общие положения
Представление переключательных функций в виде совершенных дизъюнктивных и совершенных конъюнктивных нормальных форм оказывается достаточно громоздким, особенно для функций, зависящих от большого числа переменных, поэтому на практике стараются использовать более простые эквивалентные представления, которые в общем случае называют дизъюнктивными нормальными формами (ДНФ) и конъюнктивными нормальными формами (КНФ). В настоящем разделе курса рассматривается только построение ДНФ с минимальным числом букв. Задача нахождения минимальной КНФ не рассматривается, поскольку она может быть решена путем построения отрицания минимальной ДНФ инверсии заданной функции.
Построение упрощенных представлений основано на возможности преобразования членов СДНФ заданной функции. Например, если в СДНФ входят элементарные конъюнкции 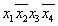 и
и 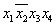 , то, вынеся за скобки общий множитель, получаем:
, то, вынеся за скобки общий множитель, получаем:
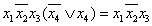
Такое преобразование двух элементарных конъюнкций в одну конъюнкцию с меньшим числом букв называют операция склеивания.
В общем случае можно определить операцию склеивания для 2L различных элементарных конъюнкций, имеющих общий множитель из (n-L) букв, где n - число переменных, из которых состоит элементарная конъюнкция. Например, после вынесения общего множителя за скобки в ДНФ
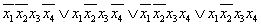
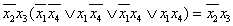 , поскольку выражение в скобках представляет собой дизъюнкцию всех элементарных конъюнкций двух переменных, которая тождественно равна единице.
, поскольку выражение в скобках представляет собой дизъюнкцию всех элементарных конъюнкций двух переменных, которая тождественно равна единице.
Заметим, что по результату склеивания можно всегда восстановить исходную совокупность элементарных конъюнкций. Восстановление выполняется с использованием последовательных действий, которые назовем операцией расширения. Эта операция выполняется путем умножения конъюнкции, полученной в результате склеивания, на дизъюнкцию каждой отсутствующей буквы и ее отрицания. Например, чтобы восстановить заданную ДНФ по конъюнкции 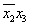 полученной в предыдущем примере, необходимо домножить ее на произведение
полученной в предыдущем примере, необходимо домножить ее на произведение 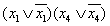 . В результате получаем
. В результате получаем 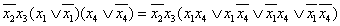 .
.
Назовем число букв, образующих конъюнкцию, рангом конъюнкции. Для обозначения ранга конъюнкции K условимся использовать выражение r(K). Отметим, что склеиваться могут только конъюнкции одинакового ранга. Между конъюнкциями различных рангов может существовать отношение покрытия. Если r(Ki) < r(Kj) и если Ki ∧ Kj = Ki, то говорят, что конъюнкция Ki покрывает конъюнкцию Kj. Например, всякая конъюнкция, получающаяся в результате склеивания, покрывает все элементарные конъюнкции, используемые для ее построения.
Назовем сумму рангов конъюнкций, входящих в ДНФ заданной функции, рангом дизъюнктивной нормальной формы. Тогда ранг ДНФ, состоящей из m дизъюнктивных членов,
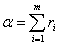
Пример 3.1.
Пусть переключательная функция φ (x1, x2,x3, x4) задана совокупностью своих элементарных конъюнкций:
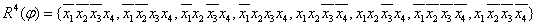
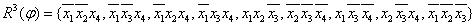
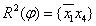
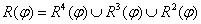 . Любое подмножество
. Любое подмножество 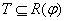 , конъюнкции которого покрывают все элементарные конъюнкции множества
R4( φ), назовем покрытием заданной функции φ.
Например, следующие три подмножества являются покрытиями заданной функции:
, конъюнкции которого покрывают все элементарные конъюнкции множества
R4( φ), назовем покрытием заданной функции φ.
Например, следующие три подмножества являются покрытиями заданной функции:
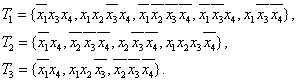
Каждое покрытие соответствует ДНФ заданной переключательной функции. Таким образом, множество различных покрытий определяет множество эквивалентных дизъюнктивных нормальных форм переключательной функции φ.
Дизъюнктивную нормальную форму, обладающую наименьшим рангом из всех ДНФ заданной переключательной функции, назовем минимальной дизъюнктивной нормальной формой (МДНФ). В рассматриваемом примере МДНФ соответствует покрытию Т3 и имеет вид 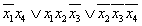 . Ранг этой ДНФ равен восьми.
. Ранг этой ДНФ равен восьми.
Анализируя элементы комплекса R(φ), можно заметить, что некоторые из них покрываются конъюнкциями меньшего ранга и что имеются элементы, которые не покрываются другими конъюнкциями. Это наблюдение позволяет нам сформулировать следующее определение. Конъюнкция K называется минималью или простым
импликантом, если в комплексе R(φ) не существует другой конъюнкции K' меньшего ранга, которая покрывает конъюнкцию K. Например, множество минималей S функции, приведенной в примере 3.1, имеет вид:
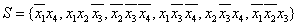
Дизъюнктивная форма, соответствующая множеству минималей, называется сокращенной дизъюнктивной нормальной формой (СкДНФ). Используя определение минимали, сформулируем следующую теорему.
| Теорема 3.1. | Любая минимальная дизъюнктивная нормальная форма состоит из минималей. |
Доказательство.
Допустим, что форма L является МДНФ функции φ и что в нее входит конъюнкция K, которая не является минималью. Тогда, согласно
определению минимали, в комплексе R(φ) должна существовать конъюнкция меньшего ранга K', которая покрывает K и является минималью. Поскольку K' покрывает K, то она покрывает все элементарные конъюнкции, покрываемые K, и, следовательно, в форме L можно конъюнкцию K заменить конъюнкцией K'. Обозначим ДНФ, полученную после такой замены, L. Формы L и L' отличаются только одной конъюнкцией, причем r(K) > r(K'). Следовательно, r(L) > r(L'). Итак, наше предположение о том, что L является МДНФ и содержит конъюнкцию, не являющуюся минималью, является неверным, что и доказывает справедливость теоремы.
Приведенная теорема дает нам основание при построении МДНФ работать с множеством минималей S вместо того, чтобы выполнять это построение, пользуясь элементами комплекса R(φ), который содержит, как правило, значительно большее число элементов, чем S. Необходимо отметить, что ранг СкДНФ может намного превышать ранг МДНФ, поэтому построение СкДНФ следует рассматривать как первый этап процедуры нахождения МДНФ заданной функции. Задачей второго этапа этой процедуры обычно является упрощение полученной СкДНФ, которое достигается за счет удаления избыточных конъюнкций из СкДНФ.
Алгоритм построения множества минималей, или СкДНФ, зависит от того, в какой дизъюнктивной форме задана функция. Как правило, функцию задают либо в СДНФ, либо в произвольной ДНФ. Построение множества минималей несколько упрощается при задании функции в виде СДНФ.
Задание дизъюнктивных нормальных форм с использованием переменных с индексами и знаками отрицания является достаточно сложным, поэтому в дальнейшем мы перейдем к форме задания ДНФ в виде совокупностей троичных кодов. Задачи, связанные с построением МДНФ, обычно являются весьма трудоемкими. Для решения подобных задач требуется выполнение большого числа простых операций, поэтому такие задачи целесообразно решать с помощью универсальных цифровых вычислительных машин. Существенно, что задание ДНФ в виде совокупностей троичных кодов соответствует естественному способу представления переключательных функций в машине.