



Метод Квайна - Мак-Класки предназначен для нахождения множества минималей (простых импликант) для функций, заданных совокупностью наборов, на которых функция равна единице, или дизъюнктивной совершенной нормальной формой. Если Cn(φ) - множество кодов,
определяющих функцию φ, то наборы 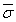 и
и  , отличающиеся значением только одного компонента σi, можно склеить и получить набор
, отличающиеся значением только одного компонента σi, можно склеить и получить набор 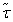 ранга n-1. Выполняя все возможные склеивания наборов
ранга n-1. Выполняя все возможные склеивания наборов 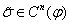 , можно построить множество наборов Cn-1(φ)
для заданной функции. Если операцию склеивания повторить для кодов τ ∈ Cn-1(φ), то можно получить множество кодов Cn-1(φ). Повторяя подобным образом операции склеивания, можно последовательно получить множества C
n-1(φ), C n-2(φ),...,C1(φ), если, конечно, они существуют. При этом коды, которые не были использованы для получения кодов меньшего ранга, т.е. коды, которые не покрываются кодами меньшего ранга, образуют искомое множество минималей.
, можно построить множество наборов Cn-1(φ)
для заданной функции. Если операцию склеивания повторить для кодов τ ∈ Cn-1(φ), то можно получить множество кодов Cn-1(φ). Повторяя подобным образом операции склеивания, можно последовательно получить множества C
n-1(φ), C n-2(φ),...,C1(φ), если, конечно, они существуют. При этом коды, которые не были использованы для получения кодов меньшего ранга, т.е. коды, которые не покрываются кодами меньшего ранга, образуют искомое множество минималей.
Чтобы упростить процедуру поиска склеивающихся кодов, используют таблицу, состоящую из n столбцов. В первый столбец таблицы заносят коды множества Cn(φ). Склеивание кодов этого множества возможно лишь в том случае, если коды отличаются значением только одного компонента. Поэтому коды в этом столбце можно разместить, разделяя их на группы так, чтобы в каждую группу входили коды, имеющие одинаковое число единиц. Группы целесообразно расположить таким образом, чтобы число единиц в кодах каждой последующей группы было
на единицу больше, чем в предыдущей. При таком размещении склеивание возможно только между кодами, расположенными в соседних группах. В результате склеивания кодов соседних групп может быть получено множество кодов ранга n-1, которые будут иметь одинаковое число единиц. Полученные коды расположим в столбце n-1, сохраняя разбиение по группам с одинаковым числом единиц и располагая группы в порядке возрастания числа единиц. Для кодов в полученном столбце можно повторить операцию склеивания для соседних групп и построить множество
кодов ранга n-2. Сохраняя разбиение на группы и упорядочение групп, в каждом из последующих столбцов можем найти множества
Cn-3(φ), Cn-4(φ),..., C1(φ).
Для того чтобы упростить отыскание минималей в полученном множестве кодов различного ранга, необходимо отмечать в таблице при каждом склеивании коды, из которых был получен код меньшего ранга. В качестве отметки может быть использована, например, галочка. В итоге, после выполнения всех возможных склеиваний, коды, не имеющие отметок, должны войти в множество минималей, поскольку они не покрываются никакими другими кодами.
В качестве иллюстрации описанного способа рассмотрим следующий пример.
Пример 3.2.
Требуется найти множество минималей для функции
φ(x1, x2,x3,х4)={0000, 0001, 1000, 0011, 0101, 0111, 1100, 1101}
из примера 3.1.
Таблица 3.1
| C4(φ) |
C3(φ) |
C2(φ) |
C1(φ) |
| 0000 ∨ |
|
|
|
0001 ∨
1000 ∨
|
000z
z000
|
0011 ∨
0101 ∨
1100 ∨
|
00z1 ∨
0z01 ∨
1z00
|
0111 ∨
1101 ∨
|
0z11 ∨
01z1 ∨
110z
z101
|
0zz1
|
|
Построим таблицу из четырех столбцов и поместим в первый столбец таблицы заданные коды, предварительно разбив их на группы по числу единиц, как это показано в табл.3.1. Выполняя операцию склеивания смежных кодов, расположенных в соседних группах, и помечая коды, использованные для склеивания, получаем коды ранга три, которые записаны во второй столбец табл.3.1. В этом столбце коды также разделены на группы с одинаковым числом единиц. Выполняя операцию склеивания для смежных кодов в соседних группах, получаем коды ранга два,
которые запишем в третий столбец. Поскольку в рассматриваемом примере получается всего один код ранга два, то процесс заканчивается, и множество кодов, не имеющих отметок в таблице, представляет собой множество минималей
Q = {000z, z000, 1z00, 110z, z101, 0zz1}.
Полученный результат может быть изображен геометрически в виде совокупности граней гиперкуба, как это показано на рис. 8.27.
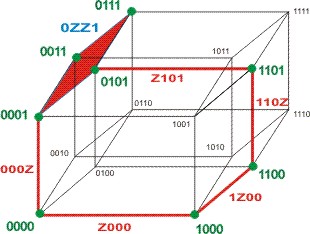
Рис.8.27
Из рисунка видно, что полученное покрытие покрывает все вершины гиперкуба, соответствующие заданной функции, и что это покрытие является избыточным, поскольку многие вершины покрываются двумя гранями.




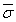 и
и  , отличающиеся значением только одного компонента σi, можно склеить и получить набор
, отличающиеся значением только одного компонента σi, можно склеить и получить набор 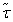 ранга n-1. Выполняя все возможные склеивания наборов
ранга n-1. Выполняя все возможные склеивания наборов 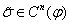 , можно построить множество наборов Cn-1(φ)
для заданной функции. Если операцию склеивания повторить для кодов τ ∈ Cn-1(φ), то можно получить множество кодов Cn-1(φ). Повторяя подобным образом операции склеивания, можно последовательно получить множества C
n-1(φ), C n-2(φ),...,C1(φ), если, конечно, они существуют. При этом коды, которые не были использованы для получения кодов меньшего ранга, т.е. коды, которые не покрываются кодами меньшего ранга, образуют искомое множество минималей.
, можно построить множество наборов Cn-1(φ)
для заданной функции. Если операцию склеивания повторить для кодов τ ∈ Cn-1(φ), то можно получить множество кодов Cn-1(φ). Повторяя подобным образом операции склеивания, можно последовательно получить множества C
n-1(φ), C n-2(φ),...,C1(φ), если, конечно, они существуют. При этом коды, которые не были использованы для получения кодов меньшего ранга, т.е. коды, которые не покрываются кодами меньшего ранга, образуют искомое множество минималей.
