 ) = f(x1,...,xn) называют монотонной, если для любых двух сравнимых наборов
) = f(x1,...,xn) называют монотонной, если для любых двух сравнимых наборов 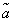 и
и 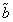 , таких, что
, таких, что 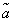 ≤
≤ 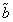 ,
справедливо f(
,
справедливо f(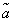 ) ≤ f(
) ≤ f(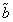 ).
).8.4.2.1. Монотонные и линейные функции
| Определение: |
Функцию f( ) = f(x1,...,xn) называют монотонной, если для любых двух сравнимых наборов ) = f(x1,...,xn) называют монотонной, если для любых двух сравнимых наборов 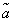 и и 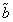 , таких, что , таких, что 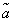 ≤ ≤ 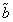 ,
справедливо f( ,
справедливо f(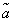 ) ≤ f( ) ≤ f(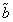 ). ). |
Все монотонные функции образуют класс М. Для отнесения произвольной функции из табл. 4.1 к этому классу необходимо сравнить ее значения на всех пяти парах сравнимых наборов: (0,0) ≤ (0,1), (0,0) ≤ (1,0), (0,0) ≤ (1,1), (0,1) ≤ (1,1), (1,0) ≤ (1,1). Среди функций двух переменных монотонными являются шесть функций: f0, f1, f3, f5, f7, f15.
Свойство линейности переключательных функций определяется как свойство полинома Жегалкина, представляющего собой формулу над функциональным базисом, {∧, ⊕, 0, 1}. Рассмотрим вначале свойства операции ⊕:
Следует отметить, что отсутствие идемпотентности распространяется на сумму любого четного (нечетного) числа слагаемых.
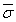 ;
частные случаи: x = x1 = x ⊕ 0;
;
частные случаи: x = x1 = x ⊕ 0; 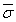 = x0 = x ⊕ 1(связь с инверсией);
= x0 = x ⊕ 1(связь с инверсией);
В общем случае для построения полинома Жегалкина произвольной ПФ нужно выполнить следующие действия:
| Определение: | Функция называется линейной, если ее полином Жегалкина имеет степень не выше первой, т. е. содержит конъюнкции длиной не более 1. |
Всякая линейная функция может быть представлена в виде линейного полинома Жегалкина:
(x1,...,xn) = a0 ⊕ a1x1 ⊕...⊕ aixi ⊕...⊕ anxn, где ai ∈ {0,1}, i = 0,1,...,n.
Все линейные функции образуют класс L. Для проверки произвольной функции на принадлежность классу L необходимо построить для нее полином Жегалкина.
Если в построенном полиноме Жегалкина хотя бы один из коэффициентов aj, j = n+1,...,(2n-1), соответствующих нелинейным конъюнктивным членам полинома, отличен от нуля, функция не принадлежит классу L, т. е. нелинейна.
Проверим на линейность некоторые функции из табл. 4.1. Очевидно, что в такой проверке не нуждаются функции f0(x,y) = 0, f3(x,y) = x, f5(x,y) = y, f6(x,y) = x ⊕ y, f15(x,y) = 1.
Функции f12(x,y) =  и f10(x,y) =
и f10(x,y) = 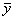 могут быть приведены к полиномам вида f12(x,y) = 1 ⊕ x и f10(x,y) = 1 ⊕ y, являющимся линейными, что указывает на линейность этих функций.
могут быть приведены к полиномам вида f12(x,y) = 1 ⊕ x и f10(x,y) = 1 ⊕ y, являющимся линейными, что указывает на линейность этих функций.
Функция равнозначности f9(x,y) = x ∼ y может быть представлена СДНФ вида xy ∨ 
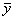 .
После замены символа дизъюнкции ∨ символом ⊕ функции mod 2, замены переменных с отрицаниями, раскрытия скобок и приведения подобных членов получим полином Жегалкина
.
После замены символа дизъюнкции ∨ символом ⊕ функции mod 2, замены переменных с отрицаниями, раскрытия скобок и приведения подобных членов получим полином Жегалкина
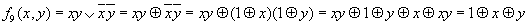
Для функции f1(x,y) = xy (конъюнкция) полином Жегалкина строится тривиально: f1(x,y) = xy = 0 ⊕ xy. Как видно, полином и соответственно функция конъюнкции нелинейны.
Теперь построим полином Жегалкина для функции f7(x,y) = x ∨ y - дизъюнкция:
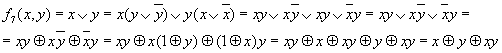
Для функции f14(x,y) = x / y - функции Шеффера полином строится достаточно просто, так как она (см. табл. 4.1) является инверсией конъюнкции:
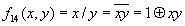 .
.
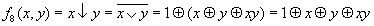 .
.
Таким образом, мы рассмотрели пять замечательных классов функций, каждый из которых вследствие замкнутости не обладает свойством функциональной полноты. Ответ о требованиях к функционально полному базису дает теорема о функциональной полноте.