|
ПРИМЕРЫ ЗАДАНИЙ МЕЖВУЗОВСКОЙ ОЛИМПИАДЫ ПО ФИЗИКЕ 2000
1. Теннисный мяч падает на тяжелую ракетку
под углом 60° к нормали и упруго отражается. Масса мяча пренебрежимо мала
по сравнению с массой ракетки. Как должна двигаться ракетка, чтобы
мяч отразился под прямым углом к первоначальной траектории?
2. Сплошной однородный цилиндр радиусом
R катится по горизонтальной плоскости, которая переходит в наклонную
плоскость (под уклон), составляющую угол a с горизонтом. Найти максимальное значение скорости V0 оси цилиндра, при которой
он перейдет на наклонную плоскость ещё без скачка.
3. Сплошной однородный
диск радиусом 10 см, имевший начальную угловую скорость 50 рад/с
( относительно оси, перпендикулярной плоскости диска и проходящей
через центр масс), кладут основанием на горизонтальную поверхность.
Сколько оборотов сделает диск до остановки, если коэффициент трения
между основанием диска и горизонтальной поверхностью m = 0,1 и не зависит от угловой скорости вращения.
4. Согласно первому закону термодинамики:
dQ
= dU + PdV , где U - внутренняя энергия, PdV
- механическая работа, производимая системой. Показать, что дифференциальное
выражение для работы dA
= PdV - не является полным дифференциалом.
5. При каких градиентах
температуры возможен нижний мираж,т.е. появление помимо предмета
его перевёрнутого изображения, расположенного ниже. ( В пустыне
это явление создаёт иллюзию водной поверхности, в которой <отражается>
предмет.)
6. Углекислый газ расширяется адиабатически
в пустоту от критического состояния до объёма, многократно превышающего
первоначальный. Оценить конечную температуру газа, если его критическая
температура равна 310С. (Коэффициенты Ван-дер-Ваальса: а = (27/8)*R*Tкр*b; b
= R*Tкр/8*Pкр )
7. В длинной вертикальной
цилиндрической трубке, закрытой с нижнего конца, может ходить без
трения поршень, масса у которого М велика по сравнению с массой
газа, заключенного внутри трубки. В положении равновесия расстояние
между поршнем и дном трубки равно l0. Определить период
малых колебаний, которые возникнут при отклонении поршня от положения
равновесия, в предположении, что они являются изотермическими, а
газ идеальным. Площадь поперечного сечения трубки S,
нормальное атмосферное давление
P0.
8. Тонкий медный
диск лежит на бесконечной проводящей плоскости. Однородное гравитационное
поле направлено перпендикулярно к плоскости. Вначале диск и плоскость
не заряжены, к ним медленно подводится заряд. Какова должна быть
плотность заряда, чтобы диск толщиной h
= 0,1 мм приподнялся над плоскостью ?
9. Протон находится внутри соленоида
круглого сечения на некотором расстоянии от его оси. В обмотке соленоида
включают ток и индукция магнитного поля становится равной B = 0.01 Тл. Пренебрегая смещением протона за время включения поля,
определить, за какое время он окажется на оси соленоида.
10. Волновая функция электрона в основном
состоянии атома водорода имеет вид 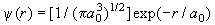 , где , где 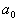 - первый боровский радиус. Найти: а) радиальную плотность
вероятности - первый боровский радиус. Найти: а) радиальную плотность
вероятности 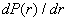 обнаружить электрон на расстоянии r от ядра (изобразить график этой функции); б) наиболее вероятное
расстояние r* электрона от ядра; в) среднее расстояние <r> электрона от ядра. обнаружить электрон на расстоянии r от ядра (изобразить график этой функции); б) наиболее вероятное
расстояние r* электрона от ядра; в) среднее расстояние <r> электрона от ядра.
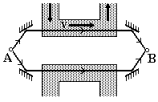
11. Свет с частотой n = 1014Гц проходит от источника А через два одинаковых трубопровода
длиной l
= 5м. Заполненных жидкостью с показателем преломления n
= 1,3. В верхнем трубопроводе жидкость движется со скоростью V, в нижнем покоится. При каком минимальном
значении V в точке В наблюдается первый интерференционный
минимум. Геометрические длины лучей в обоих случаях одинаковы.
ПРИМЕРЫ ЗАДАНИЙ МЕЖВУЗОВСКОЙ ОЛИМПИАДЫ ПО ФИЗИКЕ 2000
Untitled Document
|