Пред.Страница  След.Страница  Раздел  Содержание


8.1.1. ВВЕДЕНИЕ В ТЕОРИЮ РЕШЕТОК

8.1.1.1. Частично упорядоченные множества

Алгебраическое понятие решетки тесно связано с отношением порядка, заданным на конечном множестве, и может быть определено следующим образом.

Определение: Множество S называется  частично упорядоченным (ЧУМ), если на нем задано рефлексивное, транзитивной и антисимметричное бинарное отношение частичного порядка ρ.

Частично упорядоченное множество можно обозначить через (S, ρ) и, если не возникает двусмысленности, вместо ρ можно записать ≤, а (S, ≤) обозначить просто через S.

Определение: ЧУМ называется линейно упорядоченным (цепью), если для любых x,y ∈ S или x ≤ y, или y ≤ x, либо выполняются оба эти отношения (x = y).

Любое конечное, линейно упорядоченное множество (A, ≤) можно представить следующим образом: a1 ≤ a2 ≤ a3 ≤. . .≤ an. Мы можем также записать A как (a1, a2, . . ., an). Линейно упорядоченное множество можно изобразить графически диаграммой, в которой элементам множества соответствуют вершины. Из вершины а ведет дуга в вершину b, если a ≤ b и нет такого с, что a ≤ c ≤ b. Конечному линейно упорядоченному множеству (A, ≤) соответствует диаграмма вида (рис. 8.3)




Рис. 8.3

На таких диаграммах не принято изображать петли, отображающие рефлексивность отношения ≤, и дуги, отображающие транзитивность этого отношения.

Утверждение: Частичное упорядочение на конечном множестве может быть представлено как объединение отношений линейного порядка на некоторых подмножествах данного множества.

Любой частичный порядок можно представить изображением объединения множества диаграмм соответствующих линейно упорядоченных подмножеств. Полученная таким образом диаграмма называется диаграммой Хасса.


Рис. 8.4

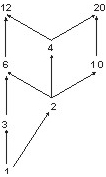
Пример1.1.

Пусть на множестве S={1,2,3,4,6,10,12,20} задано отношение ρ={(x, y):х делитель y}. Выделим все линейно упорядоченные подмножества S:(1, 3, 6, 12), (1, 2, 6, 12), (1, 2, 4, 12), (1, 2, 4, 20), (1, 2, 10, 20). Объединение диаграмм, построенных для этих подмножеств, дает диаграмму Хасса, показанную на рис. 8.4. Если задано (S, ≤) и B – подмножество S: B ⊆ S, можно определить верхнюю и нижнюю грани подмножества В.

Определение: Верхней гранью двухэлементного подмножества B={a,b}, a,b ∈ S, называется элемент h ∈ S, такой, что a ≤ h, b ≤ h. Соответственно,
нижней граньюдвухэлементного подмножества B={a, b}, a, b ∈ S, называется элемент l ∈ S, такой, что l ≤ a, l ≤ b.

Определение: Если некоторая из верхних граней H подмножества B={a,b} удовлетворяет неравенству H ≤ h, где h - произвольная верхняя грань подмножества B={a,b}, то ее называют наименьшей верхней гранью (supremum) подмножества B и обозначают H=sup ({a,b}). Соответственно, если некоторая из нижних граней L подмножества B={a,b} удовлетворяет неравенству l ≤ L, где l - произвольная нижняя грань, то ее называют наибольшей нижней гранью (infimum) подмножества B и обозначают L=inf ({a,b}).

Введенные понятия хорошо иллюстрируются на языке диаграмм Хасса:
x ≤ y , если и только если на диаграмме существует путь из вершины x в вершину y; верхняя грань подмножества B={a,b} на диаграмме соответствует вершине, в которую есть путь как из a, так и из b; нижняя грань подмножества B={a,b} соответствует вершине, из которой есть путь как в a, так и в b.

Пример1.2.

Рассмотрим ЧУМ, представленное диаграммой Хасса на рис. 8.4. Подмножество B={3,6} имеет две верхние грани: h1=6 и h2=12, одна из которых является наименьшей: H=sup({3,6})=h1=6. Это же подмножество имеет две нижние грани:l1=1 и l2=3, одна из которых является наибольшей: L=inf({3,6})=l2=3. Подмножество B={6,4} имеет одну верхнюю грань h1=12, которая, естественно, будет наименьшей верхней гранью H=sup ({6,4})=12, и две нижние грани l1=2, l2=1, одна из которых будет наибольшей: L=inf ({6,4})=l1= 2. Подмножество B={6,10} имеет те же две нижние грани l1=2, l2=1 и ту же наибольшую нижнюю грань L=inf ({6,10})=l1= 2, однако не имеет ни одной верхней грани !

Пред.Страница  След.Страница    Раздел    Содержание