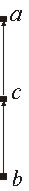Решетки

8.1.1.2. Решетки

Определение:

Решеткой называется множество (S, ≤),в котором для любого двухэлементного подмножества B ⊆ S существует наименьшая верхняя грань H и наибольшая нижняя грань L. Иначе говоря, решетка - это алгебраическая система (S, ≤, ∧, ∨) с одним бинарным отношением ≤ и двумя бинарными операциями:
x ∧ y = L = inf ({x,y}) (конъюнкция),
x ∨ y = H = sup ({x,y}) (дизъюнкция),
определенными на множестве всех возможных двухэлементных подмножест B ⊆ S.

Пример1.3.

Пусть задано множество S из трех различных целых чисел a, b, c. На этом множестве отношение ≤ (меньше или равно) задает частичный порядок. Предположим, что значения a, b, c таковы, что линейный порядок на множестве можно изобразить диаграммой на рис. 8.5. Если на множестве целых чисел S = {a, b, c} можно определить для любых x, y ∈ S две бинарные операции:

x ∧ y = inf ({x,y}) = min (x,y),
x ∨ y = sup ({x,y}) = max (x,y), то это множество представляет собой решетку.


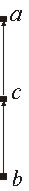	a)	b)
Рис. 8.5	Рис. 8.6

Возможны две причины, по которым частично упорядоченное множество (S, ≤) не является решеткой.

Причина 1.
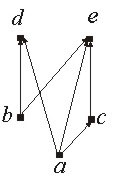
Существует хотя бы одно из двухэлементных подмножеcтв B ⊆ S, не имеющее верхней или нижней грани. На диаграмме на рис. 8.6, а. подмножества {d, e},{d, c} не имеют верхней грани, подмножество {b,c} не имеет нижней грани.
По этой же причине не является решеткой ЧУМ из примера 1.1. Как следует из диаграммы Хасса (рис. 8.4), для любого двухэлементного подмножества B ⊆ S существует единственная наибольшая нижняя грань, однако для подмножеств {3,10},{3,20},{6,10},{6,20},{12,10},{12,20} не существует верхняя грань и, следовательно, для этих пар элементов не определена операция ∨.

Причина 2.
Существует хотя бы одно из двухэлементных подмножеств B ⊆ S, для которого наибольшая нижняя (наименьшая верхняя) грань не единственна. На диаграмме на рис. 8.6, б все двухэлементные подмножества B ⊆ S имеют наименьшие верхние и наибольшие нижние грани, однако подмножество {b,c} имеет две несравнимые (не связанные отношением ≤) наименьшие верхние грани d и e; подмножество {d,e} имеет две несравнимые наибольшие нижние грани b и c.

Пример 1.4.
Рассмотрим множество V_n двоичных векторов длины n. Пусть на этом множестве задан частичный порядок с помощью отношения ν ≤ ω, если в векторе ω единицы стоят на всех тех местах, на которых они стоят в векторе ν (и, может быть, еще на некоторых). Например, при n = 3: (010) ≤ (011), однако векторы (010) и (100) несравнимы в смысле заданного отношения ≤.
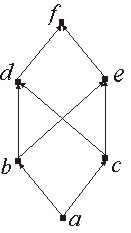
Диаграмма Хасса для ЧУМ (V₃, ≤) показана на рис. 8.7. Определим на множестве (V_n, ≤) две бинарные операции:ν ∧ ω - это вектор, в котором единицы стоят на тех и только тех местах, где единицы есть как в ν, так и в ω; ν ∨ ω - это вектор, в котором единицы стоят на тех и только тех местах, где есть единицы либо в ν, либо в ω.
Например, при n = 3: (011) ∧ (101) = (001), (011) ∨ (101) = (111).

Рис.8.7

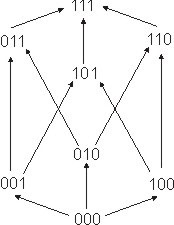
Простым перебором всех двухэлементных подмножеств нетрудно доказать, что множество (V₃, ≤, ∧, ∨) является решеткой.
Если на заданном ЧУМ (S, ≤) определены бинарные операции ∧ и ∨, то можно выявить ряд свойств этих операций,не зависящих от природы множества S. Эти свойства заключаются в следующем.

1. Любой элемент решетки x ∈ S идемпотентен по отношению к обеим операциям:

x ∧ x = x (аксиома А1а),
x ∨ x = x (аксиома А1б).
Очевидно, что наибольшая нижняя и наименьшая верхняя грани "подмножества" {x,x} есть x.

2. Обе операции коммутативны:
x ∧ y = y ∧ x (аксиома А2а),
x ∨ y = y ∨ x (аксиома А2б).

Доказательство коммутативности следует из самого определения этих операций. Как в определении операции ∧ (поиск наибольшей нижней грани двухэлементного подмножества {x,y}), так и в определении операции ∨ (поиск наименьшей верхней грани двухэлементного подмножества {x,y}) отношение порядка между элементами x и y сохраняется независимо от последовательности их написания в подмножестве {x,y}.

3. Обе операции ассоциативны:
(x ∧ y) ∧ z = x ∧ (y ∧ z) (аксиома А3а),
(x ∨ y) ∨ z = x ∨ (y ∨ z) (аксиома А3б).
Для доказательства ассоциативности операции ∧ необходимо убедиться в том, что (x ∧ y) ∧ z - наибольшая нижняя грань трехэлементного подмножества {x,y,z}, т.е. элемент L, являющийся результатом двойного применения операции ∨: L=(x ∨ y) ∨ z, меньше или равен любого из элементов x, y, z и в то же время больше или равен любого из элементов l, являющихся нижней гранью для элементов x, y, z: l ≤ x, l ≤ y, l ≤ z, l ≤ L.
Действительно, так как элемент L=(x ∧ y) ∧ z - это наибольшая нижняя грань подмножества {L_xy, z}, где L_xy= x ∧ y, то L ≤ L_xy и L ≤ z.
В свою очередь из отношения L ≤ L_xy= x ∧ y следует, что L ≤ x и L ≤ y.
Итак, можно считать установленным, что наибольшая нижняя грань удовлетворяет неравенствам L ≤ x, L ≤ y, L ≤ z. Но если нижняя грань удовлетворяет неравенствам L ≤ x и L ≤ y, то L ≤ x ∧ y= L_xy. Если выполняется еще и отношение L ≤ z, то L ≤ (x ∧ y) ∧ z = L_xy ∧ z = L , т. е. наибольшая нижняя грань L больше или равна любой из нижних граней. Из коммутативности операции ∧ следует:
x ∧ (y ∧ z) = x ∧ L_yz = L_yz ∧ x = (y ∧ z) ∧ x.
На основании предыдущих рассуждений это означает, что элемент L = x ∧ (y ∧ z) = (y ∧ z) ∧ x – наибольшая нижняя грань трехэлементного подмножества {y, z, x}. Поскольку подмножества {x, y, z}, {y, z, x} эквивалентны, то их наибольшие нижние грани L = (x ∧ y) ∧ z и L = x ∧ (y ∧ z) - совпадают. Тем самым ассоциативность операции ∧ доказана.

Ассоциативность операции ∨ может быть доказана аналогично

Пред.Страница След.Страница Раздел Содержание