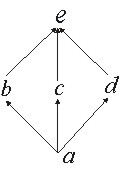
Рис.8.8
8.1.1.3. Дистрибутивные решетки
Покажем, что не все решетки являются дистрибутивными, на следующем примере.

Пример 1.5.
Исследуем на дистрибутивность решетку, приведенную
на рис.8.8. Проверим свойство дистрибутивности операции ∧ по отношению к операции ∨:
x ∧ (y ∨ z) = (x ∧ y) ∨ (a ∧ z) для x = b, y = d и z = c.
"Вычислим" левую часть этого выражения: x ∧ (y ∨ z) = b ∧ (d ∨ c) = b ∧ e = b.
Теперь "вычислим" правую часть выражения: (x ∧ y) ∨ (a ∧ z) = (b ∧ d) ∨ (b ∧ c) = a ∨ a = a.
Левая и правая части выражения различны, следовательно, рассмотренная
решетка не дистрибутивна.
Пример 1.6.
Исследуем на дистрибутивность решетку, приведенную
в примере 1.4 (диаграмма на рис. 8.7).
Проверим свойство дистрибутивности операции ∨ по отношению к операции ∧:
x ∨ (y ∧ z) = (x ∨ z) ∧ (x ∨ y) для x = 011, y = 010, z = 110.
"Вычислим" левую часть выражения: 011 ∨ (010 ∧ 110) = 011 ∨ 010 = 011.
Теперь "вычислим" правую часть выражения: (011 ∨ 010) ∧ (011 ∨ 110) = 011 ∧ 111 = 011.
Совпадение обеих частей выражения означает, что операция ∨ дистрибутивна по отношению к операции ∧ для x = 011, y = 010, z = 110.
Полный перебор всех возможных "троек" элементов множества и проверка для каждой "тройки" обоих свойств дистрибутивности
позволяют утверждать, что рассмотренная решетка дистрибутивна.
Свойства решетки зависят также от того, существуют ли в ней единичные элементы
по отношению к операциям ∧ и ∨.
| Теорема 1.1. | Пусть и существует единичный элемент по отношению к операции Тогда единичный элемент единственен. |
Доказательство теоремы проведем "от противного".
Доказательство.
Предположим, что существуют два различных единичных элемента e и e',
тогда для любого x ∈ S справедливы равенства x ![]() e = x и x
e = x и x ![]() e' = x.
e' = x.
Подставим x = e' в первое равенство, x = e - во второе, тогда e' ![]() e = e' и e
e = e' и e ![]() e' = e.
e' = e.
Но из свойства коммутативности операции ![]() следует e'
следует e' ![]() e = e
e = e ![]() e',
e',
поэтому e' = e, что и требовалось доказать.
Единичный элемент по отношению к операции ∧ (обозначим его e∧) должен удовлетворять равенству
Иначе говоря, для произвольного элемента x ∈ S наибольшей нижней гранью двухэлементного подмножества {x,e}
должен быть сам элемент x. Интуитивно ясно, что единичный элемент по отношению
к операции ∧ должен быть наибольшим элементом решетки, а это, в свою очередь, означает,
что элемент e∧ должен быть наименьшей верхней гранью для любого подмножества {x,e∧}.
Операция нахождения наименьшей верхней грани была ранее определена как
бинарная:
однако она может быть естественным образом расширена так, что результатом ее выполнения будет наименьшая верхняя грань
всей решетки:
иначе говоря, наибольший элемент решетки S.
Аналогичными рассуждениями нетрудно показать, что единичный элемент по отношению к операции ∨ (обозначим его e∨) должен быть наибольшей нижней гранью решетки в целом:
иначе говоря, наименьший элемент решетки S.
Пример 1.7.
В решетке S из примера 1.4 (диаграмма на рис. 8.7) элементом e∧ является вектор 111, а элементом e ∨
- вектор 000.
Таким образом, в соответствии с определением операций ∧ и ∨ как бинарных операций и теоремой 1.1 в решетке существуют единственные
единичные элементы по отношению к операциям ∧ и ∨(e∧ и e∨ соответственно), обладающие следующими свойствами:
x ∨ e∨ = e∨ ∨ x = x (аксиома А5б).