8.2.1. Алгебра переключательных функций
Прейдем к рассмотрению свойств множества функций P(n). Прежде всего отметим, что это множество является частично упорядоченным, поскольку для некоторых функций φ1(
) и φ2() можно установить отношение частичного порядка (≤). Переключательные функции φ1() и φ2() связаны отношением частичного порядка φ1() ≤ φ2(), если на каждом наборе значений переменных 
φ1() ≤ φ2().
Затем определим на этом множестве операции нахождения наибольшей нижней и наименьшей верхней граней.
Согласно определению, каждая переключательная функция из множества P(n) может принимать только значение из множества B(2).
Если определить операции конъюнкции, дизъюнкции и отрицания с помощью таблиц 2.3 и.2.4 , то путем подстановки нетрудно убедиться, что все аксиомы, рассмотренные в разделе 1, справедливыми для этих операций. Например, подставляя вместо x вначале 0, а затем 1 в выражение 1 ∧ x = x, убеждаемся, что это равенство справедливо для любого x ∈ B(2).
x2 0 0 1 1 0 1 0 1 0 0 0 1 0 1 1 1
Таблица 2.3
x1
x1 ∧ x2
x1 ∨ x2
0 1 1 0
Таблица 2.4
x
Используя введенные операции, можно выполнять операции над значениями различных функций, соответствующих одному и тому же набору аргументов . Следовательно, на множестве P(n) можно определить операции конъюнкции и дизъюнкции, соответствующие нахождению наибольшей нижней и наименьшей верхней граней, следующем образом. Результатом конъюнкции функций φ1() ∧ φ2() является функция phi;3(), значения которой получаются путем вычисления конъюнкции значений φ1() ∧ φ2() на всех наборах . Результатом дизъюнкции функций φ1() ∨ φ2() является функция φ4(), значения которой получаются путем вычисления дизъюнкции значений φ1() ∨ φ2() на всех наборах .
Таким образом, можно сделать вывод, что частично упорядоченное множество P(n) с определенными на нем операциями конъюнкции и дизъюнкции представляет собой алгебраическую решетку.
Далее можно утверждать, что при таком определении операций функция, принимающая значение 1 на всех наборах значений переменных , представляет собой наибольший элемент решетки - φ(1), а функция, принимающая значение 0 на всех наборах ,- наименьший элемент решетки - φ(0).
Более того, для каждой функции в множестве P(n) существует инверсный элемент, который вычисляется путем инвертирования каждого из значений функции φ().
Примеры выполнения операций, а также элементы φ(0) и φ(1) приведены в таблице 2.5.
000 001 010 011 100 101 110 111 0 0 1 1 0 1 0 1 0 1 0 1 1 0 1 1 0 0 0 1 0 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 1 0 1 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0
Таблица 2.5
x=(x1x2x3)
φ1
φ2
φ3 = φ1∧ φ2
φ4 = φ1∧ φ2
φ5 =
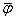1
φ(1)
φ(0)
Для введенных операций конъюнкции и дизъюнкции для переключательных функций выполняются законы дистрибутивности. Справедливость этого утверждения основывается на свойствах операций конъюнкции и дизъюнкции, определенных на множестве B(2). Выполнение законов дистрибутивности в B(2) нетрудно проверить с помощью подстановки значений переменных.
Итак, множество переключательных функций P(n) с определенными на нем операциями конъюнкции, дизъюнкции, отрицания, наибольшим и наименьшим элементами представляет собой дистрибутивную решетку с дополнениями (булеву алгебру), которую называют алгеброй переключательных функций.
Переменную xi в функции φ( x1,…, xi-1, xi, xi+1,…, xn) называют несущественной, если φ( x1,…, xi-1, 1 ,xi+1,…, xn)= φ( x1,…, xi-1, 0 ,xi+1,…, xn) при любых значениях остальных переменных. Это означает, что изменение значения переменной xi не изменяет значения функции, поэтому эту переменную можно исключить из числа аргументов и рассматривать заданную функцию, как функцию, зависящую от n-1 переменной. Несущественные переменные можно не только удалять, но и добавлять к аргументам функции. Следовательно, если заданы две функции φ( x1,…, xk) и φ( x1,…, xl), зависящие от разного числа переменных и k < l, то добавляя к функции с меньшим числом аргументов l-k несущественных переменных, можно получить функции с одинаковым количеством аргументов. Описанный прием позволяет рассматривать операции конъюнкции и дизъюнкции как операции, определенные на множестве переключательных функций с определенными на нем операциями конъюнкции, дизъюнкции и отрицания называют алгеброй переключательных функций.
С ростом числа переменных таблица, задающая переключательную функцию, сильно усложняется. Чтобы избежать
усложнения таблицы, в некоторых случаях функцию задают множеством номеров двоичных наборов, на которых она равна единице. Например, функция, приведенная в таблице 2.1, может быть задана в виде следующей совокупности двоичных наборов: