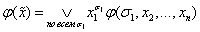i φ(x1,..., xi-1, xi, xi+1,..., xn) =
i φ(x1,..., xi-1, xi, xi+1,..., xn) =  i φ(x1,..., xi-1, 0, xi+1,..., xn).
i φ(x1,..., xi-1, 0, xi+1,..., xn). 8.2.2. Аналитическая запись переключательных функций
Способ, предполагающий перечисление наборов, на которых функция принимает значение 1, особенно удобен для функций, имеющих небольшое число единиц в таблице. В некоторых случаях существенно упростить способ задания функции удается с помощью аналитической записи, когда переключательную функцию представляют в виде некоторой логической формулы. Строго говоря, при рассмотрении аналитических представлений фактически мы имеем дело не с переключательными функциями, а с представляющими их формулами, которых значительно больше, чем переключательных функций, поскольку каждой переключательной функции соответствует множество формул. Обычно множество различных формул, соответствующих рассматриваемой переключательной функции, получают с помощью эквивалентных преобразований, основанных на свойствах булевых алгебр. При этом две формулы считаются эквивалентными, если они представляют одну и ту же переключательную функцию.
В связи с очевидным соответствием переключательных функций и представляющих их формул в дальнейшем изложении этот вопрос не будет обсуждаться, хотя следует помнить, что логическая схема реализует на своем выходе переключательную функцию, а структура логической схемы определяется видом формулы, представляющей эту функцию.
Переключательные функции обладают интересными, с точки зрения практического применения, свойствами. Прежде чем сформулировать эти свойства, рассмотрим несколько вспомогательных утверждений.
8.2.2.1. Разложение переключательных функций по одной переменной
| Лемма 2.1. | Для любой переключательной функции справедливо равенство: xi φ(x1, ..., xi-1, xi, xi+1, ..., xn) = xi φ(x1,..., xi-1, 1, xi+1, ..., xn). |
Доказательство.
Справедливость этого равенства доказывается путем подстановки различных значений xi.
При xi = 0 имеем:
0 = 0
При xi = 1 получаем:
φ(x1, ..., xi-1, 1, xi+1,..., xn) = φ(x1,..., xi-1, 1, xi+1, ..., xn)
Поскольку значения левой и правой части рассматриваемого выражения совпадают при всех значениях xi, то равенство справедливо.
| Лемма 2.2. | Для любой переключательной функции справедливо равенство: xi ∨ φ(x1,..., xi-1, xi, xi+1,..., xn) = xi ∨ φ(x1,..., xi-1, 0, xi+1,..., xn). |
Доказательство.
При xi = 0 имеем:
φ(x1,..., xi-1, 0, xi+1,..., xn) =
φ(x1,..., xi-1, 0, xi+1,..., xn)
1 = 1
Следующие два утверждения доказываются аналогично леммам 2.1 и 2.2, поэтому рекомендуем выполнить доказательства самостоятельно.
| Лемма 2.3. |
 i φ(x1,..., xi-1, xi, xi+1,..., xn) = i φ(x1,..., xi-1, xi, xi+1,..., xn) =  i φ(x1,..., xi-1, 0, xi+1,..., xn). i φ(x1,..., xi-1, 0, xi+1,..., xn). |
| Лемма 2.4. |
 i ∨ φ(x1,..., xi-1, xi, xi+1,..., xn) = i ∨ φ(x1,..., xi-1, xi, xi+1,..., xn) =  i ∨ φ(x1,..., xi-1, 1, xi+1,..., xn). i ∨ φ(x1,..., xi-1, 1, xi+1,..., xn). |
После доказательства равенств лемм 2.1 - 2.4 можно перейти к изучению разложений переключательных функций по переменным.
| Теорема 2.1. |
Любую переключательную функцию можно разложить относительно операции дизъюнкции по одному из аргументов следующим образом: i φ(x1,..., xi-1, 0, xi+1,..., xn). i φ(x1,..., xi-1, 0, xi+1,..., xn).
|
Доказательство.
= φ(x1,..., xi-1, xi, xi+1,..., xn)1 =
= φ(x1,..., xi-1, xi, xi+1,..., xn)(xi ∨  i) =
i) =
= φ(x1,..., xi-1,xi,xi+1,..., xn)xi ∨ (x1,..., xi-1, xi, xi+1,..., xn)  i =
i =
= φ(x1, ..., xi-1, 1, xi+1,..., xn)xi ∨ (x1,..., xi-1, xi, xi+1,...,xn)  i =
i =
= φ(x1,..., xi-1, 1, xi+1,..., xn)xi ∨ (x1,..., xi-1, 0, xi+1,..., xn) i
i
Используя леммы 2.2 и 2.4, нетрудно доказать справедливость разложения по одному из аргументов относительно операции конъюнкции.
| Теорема 2.2. |
Любую переключательную функцию можно разложить относительно операции конъюнкции по одному из аргументов следующим образом: i ∨ φ(x1,..., xi-1, 1, xi+1,..., xn)). i ∨ φ(x1,..., xi-1, 1, xi+1,..., xn)).
|
Для удобства дальнейшего изложения введем обозначения. Пусть:
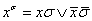 (2.1)
(2.1)
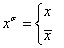
при σ = 1
при σ = 0
Пользуясь этими обозначениями, можно записать дизъюнктивное разложение по одной переменной, например по переменной х1, так:
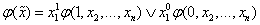 (*)
(*)