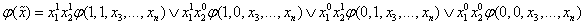
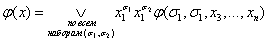
8.2.2.2. Разложение переключательных функций по k- переменным
Если теперь в выражении (*) функции φ(1, x2,..., xn) и
φ(0, x2,..., xn) разложить по переменной x2, то получим дизъюнктивное разложение функции по двум переменным:
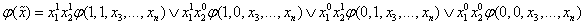
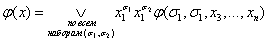
Произведения вида x1σ1 x2σ2...xlσl
называют конъюнкциями l переменных и записывают в векторной форме следующим образом:
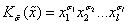
 определяет, какие переменные
образуют конъюнкцию, а набор
определяет, какие переменные
образуют конъюнкцию, а набор  задает порядок расстановки знаков инверсии над ними.
задает порядок расстановки знаков инверсии над ними.
Например:
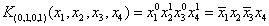
Разобьем вектор переменных  = (x1, x2, ..., xn) на два подвектора
= (x1, x2, ..., xn) на два подвектора  1 и
1 и  2 таким образом, чтобы подвектор
2 таким образом, чтобы подвектор  1 состоял из k переменных,
а подвектор
1 состоял из k переменных,
а подвектор  2 из n - k переменных:
2 из n - k переменных:
 1 = (x1, x2, ..., xk)
и
1 = (x1, x2, ..., xk)
и
 2 = (xk+1, xk+2, ..., xn).
2 = (xk+1, xk+2, ..., xn).
Такому разбиению вектора переменных соответствует разбиение вектора значений  = (σ1, σ2,..., σn) также на два подвектора:
= (σ1, σ2,..., σn) также на два подвектора:
 1 = (σ1, σ2,..., σk)
и
1 = (σ1, σ2,..., σk)
и
 2 = (σk+1, σk+2, ..., σn).
2 = (σk+1, σk+2, ..., σn).
Пользуясь этими обозначениями, сформулируем теорему об общем виде дизъюнктивного разложения.
| Теорема 2.3. |
Любую переключательную функцию, зависящую от n переменных, можно представить в виде дизъюнктивного разложения по
k ≤ n переменным: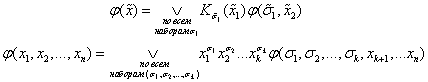 (2.2) |
Доказательство.
Справедливость теоремы доказывается индукцией по числу переменных разложения k. Возможность разложения при
k = 1 доказана в теореме 2.1, поэтому предположим, что разложение справедливо для k = L :
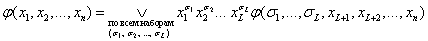
(2.3)
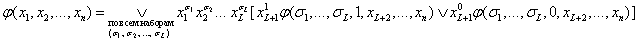
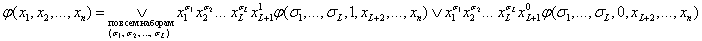
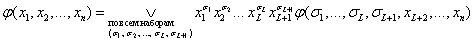
Следствие.
Любую переключательную функцию можно представить в виде дизъюнктивного разложения по k = n переменным:
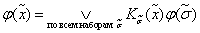
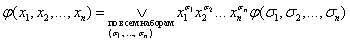
Выражение вида 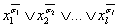 называют дизъюнкцией l переменных и обозначают:
называют дизъюнкцией l переменных и обозначают:
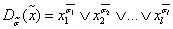
Пользуясь методом индукции, можно доказать теорему, аналогичную теореме 2.3, для конъюнктивного разложения по k переменным.
| Теорема 2.4. |
Любую переключательную функцию, зависящую от n переменных, можно представить в виде конъюнктивного разложения по
k ≤ n переменным: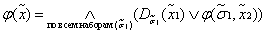 или 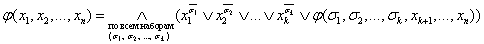 |
Следствие.
Любую переключательную функцию можно представить в виде конъюнктивного разложения по k = n переменным:
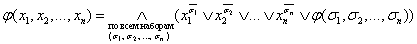
Полученные в настоящем параграфе разложения являются основой для построения аналитических выражений переключательных функций.