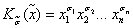
8.2.3. Совершенные дизъюнктивные и конъюнктивные нормальные формы
Прежде чем перейти к изучению аналитических форм записи, рассмотрим две простейшие функции: элементарную конъюнкцию и элементарную дизъюнкцию.
8.2.3.1. Элементарные конъюнкции и дизъюнкции
Из этой записи следует, что существует всего 2n различных элементарных конъюнкций n переменных, поскольку каждая конъюнкция определяется одним двоичным набором  , состоящим из n компонентов.
, состоящим из n компонентов.
В дальнейшем нам потребуется следующее свойство функции xσ.
| Лемма 2.5. |
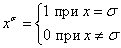
|
Доказательство.
Справедливость этого утверждения нетрудно показать с помощью подстановки значений x в выражение (2.1). При x = σ имеем:
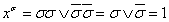
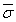 и тогда получаем:
и тогда получаем:
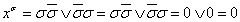
Рассмотрим теперь два свойства элементарных конъюнкций.
| Теорема 2.5. |
Элементарная конъюнкция 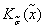 равна единице только в том случае,когда набор равна единице только в том случае,когда набор  совпадает с набором значений переменных x. совпадает с набором значений переменных x.
|
Доказательство.
Условимся считать набором значений переменных вектор 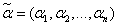 .
Если набор
.
Если набор 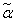 совпадает с набором
совпадает с набором  , то αi = σi для всех i.
Тогда каждый член конъюнкции
, то αi = σi для всех i.
Тогда каждый член конъюнкции 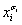 согласно лемме 2.5, равен 1,
а конъюнкция n единиц также равна 1.
Пусть теперь
согласно лемме 2.5, равен 1,
а конъюнкция n единиц также равна 1.
Пусть теперь 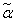 не совпадает с
не совпадает с  . Это означает, что имеется хотя бы один компонент αi ≠ σi. Тогда член конъюнкции
. Это означает, что имеется хотя бы один компонент αi ≠ σi. Тогда член конъюнкции 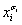 , согласно лемме 2.5, будет равен 0, и мы получим конъюнкцию вида 1 1 . . . 1 0 1 . . . 1, которая равна 0.
, согласно лемме 2.5, будет равен 0, и мы получим конъюнкцию вида 1 1 . . . 1 0 1 . . . 1, которая равна 0.
Согласно теореме 2.5, в таблице, задающей элементарную конъюнкцию, должна быть всего одна единица в столбце значений функции. Эта единица расположена в строке, отмеченной двоичным набором, совпадающим с набором  . Таким образом, каждому набору в таблице соответствует единственная элементарная конъюнкция, равная единице на этом наборе. Для того чтобы построить эту элементарную конъюнкцию, нужно расставить инверсии над переменными согласно заданному набору. Например, конъюнкция, равная единице на наборе (0, 1, 1, 1, 0), имеет вид:
. Таким образом, каждому набору в таблице соответствует единственная элементарная конъюнкция, равная единице на этом наборе. Для того чтобы построить эту элементарную конъюнкцию, нужно расставить инверсии над переменными согласно заданному набору. Например, конъюнкция, равная единице на наборе (0, 1, 1, 1, 0), имеет вид: 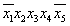 .
.
| Теорема 2.6. |
Конъюнкция двух различных элементарных конъюнкций n переменных равна нулю: 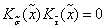 . . |
Доказательство.
Наборы  и
и 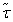 должны отличаться хотя бы одним компонентом, поскольку заданные элементарные конъюнкции различны. Пусть σi ≠ τi и σj = τj для всех j ≠ i. Тогда, если σi ≠ τi, то σj =
должны отличаться хотя бы одним компонентом, поскольку заданные элементарные конъюнкции различны. Пусть σi ≠ τi и σj = τj для всех j ≠ i. Тогда, если σi ≠ τi, то σj = 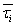 и, следовательно
и, следовательно 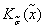 , содержит член
, содержит член 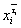 , a
, a 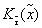 -
- 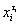 .
Конъюнкция
.
Конъюнкция 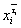
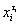 всегда равна нулю,поэтому равенство (2.8) справедливо.
всегда равна нулю,поэтому равенство (2.8) справедливо.
Из такой записи видно, что существует 2n различных элементарных дизъюнкций.
Два набора называются противоположными, если все компоненты одного из них можно получить с помощью инверсии компонентов другого набора. Например, наборы 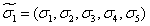 и
и 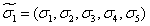 противоположны.
противоположны.
| Теорема 2.7. |
Элементарная дизъюнкция 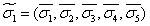 равна нулю только в том случае, когда набор равна нулю только в том случае, когда набор  является противоположным набору
значений переменных. является противоположным набору
значений переменных. |
Доказательство.
Пусть набор 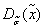 является набором значений переменных.
Если
является набором значений переменных.
Если 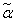 является противоположным набором для
является противоположным набором для  , то
, то 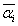 = σi для всех i, и после подстановки значений σi =
= σi для всех i, и после подстановки значений σi = 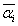 в (2.9) получим, согласно лемме 2.5, что все члены дизъюнкции равны 0. Если же
в (2.9) получим, согласно лемме 2.5, что все члены дизъюнкции равны 0. Если же 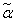 не является противоположным набором для
не является противоположным набором для  , то хотя бы один компонент αi = σi , и при подстановке значений
, то хотя бы один компонент αi = σi , и при подстановке значений  в (2.9) мы получим член
в (2.9) мы получим член 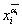 , который при xi = αi, согласно лемме 2.5, равен 1. Следовательно, на таком наборе
, который при xi = αi, согласно лемме 2.5, равен 1. Следовательно, на таком наборе 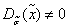
Согласно теореме 2.7, в таблице, задающей элементарную дизъюнкцию, должен быть всего один ноль в столбце значений функций. Этот ноль расположен в строке таблицы, отмеченной набором, противоположным набору  . Следовательно, каждому набору соответствует единственная элементарная дизъюнкция, равная нулю на этом наборе. Для того чтобы построить эту дизъюнкцию, нужно инвертировать компоненты заданного набора и расставить знаки над переменными согласно противоположному набору. Например, дизъюнкция, равная нулю на наборе (0, 1, 1, 1, 0), имеет вид:
. Следовательно, каждому набору соответствует единственная элементарная дизъюнкция, равная нулю на этом наборе. Для того чтобы построить эту дизъюнкцию, нужно инвертировать компоненты заданного набора и расставить знаки над переменными согласно противоположному набору. Например, дизъюнкция, равная нулю на наборе (0, 1, 1, 1, 0), имеет вид: 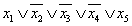 .
.