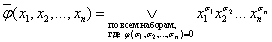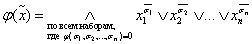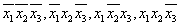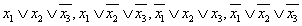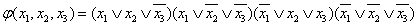Возможность аналитической записи переключательных функций показывают следующие две теоремы.
| Теорема 2.8. |
Любую переключательную функцию можно представить в совершенной дизъюнктивной нормальной форме (СДНФ) и, притом, единственным образом.
|
Прежде чем приступить к доказательству теоремы, упростим выражение (2.4). Для этого проанализируем правую часть этого выражения. Если 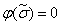 , то конъюнкция
, то конъюнкция 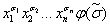 всегда равна нулю независимо от значений элементарной конъюнкции. Следовательно, такие члены из правой части выражения (2.4) можно удалить, поскольку они не влияют на результат дизъюнкции. Если же
всегда равна нулю независимо от значений элементарной конъюнкции. Следовательно, такие члены из правой части выражения (2.4) можно удалить, поскольку они не влияют на результат дизъюнкции. Если же 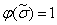 , то коэффициент 1 не влияет на величину конъюнкции
, то коэффициент 1 не влияет на величину конъюнкции 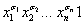 .
Учитывая сказанное СДНФ, можно записать в следующем виде:
.
Учитывая сказанное СДНФ, можно записать в следующем виде:
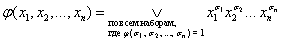
Докажем вначале, что произвольную функцию 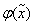 можно представить в виде СДНФ.
Для этого покажем, что значение функции
можно представить в виде СДНФ.
Для этого покажем, что значение функции 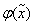 для произвольного набора можно
получить из правой части выражения (2.10). Вначале возьмем набор
для произвольного набора можно
получить из правой части выражения (2.10). Вначале возьмем набор 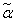 , что φ(α) = 0. При этом все элементарные конъюнкции в правой части выражения (2.10) равны нулю, так как ни один
набор
, что φ(α) = 0. При этом все элементарные конъюнкции в правой части выражения (2.10) равны нулю, так как ни один
набор  такой, что
такой, что 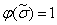 , не совпадает с набором
, не совпадает с набором 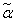 .
Рассмотрим теперь набор
.
Рассмотрим теперь набор 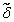 такой, что
такой, что 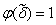 . В этом случае в правой части (2.10) найдется одна конъюнкция, у которой
. В этом случае в правой части (2.10) найдется одна конъюнкция, у которой 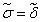 . Значение этой конъюнкции на наборе
. Значение этой конъюнкции на наборе 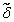 равно 1. Следовательно, и в этом случае в правой части (2.10) получается заданное значение функции.
равно 1. Следовательно, и в этом случае в правой части (2.10) получается заданное значение функции.
Покажем теперь единственность СДНФ. Каждому набору  ,
для которого
,
для которого 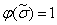 , соответствует единственная элементарная конъюнкция. Следовательно, совокупности наборов, на которых функция равна единице, соответствует единственная совокупность элементарных конъюнкций, являющаяся СДНФ заданной функции.
, соответствует единственная элементарная конъюнкция. Следовательно, совокупности наборов, на которых функция равна единице, соответствует единственная совокупность элементарных конъюнкций, являющаяся СДНФ заданной функции.
| Теорема 2.9. |
Любую переключательную функцию можно представить в совершенной конъюнктивной нормальной форме (СКНФ) и, притом, единственным образом.
|
Доказательство.
Поскольку инверсия функции 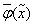 равна единице на тех наборах, на которых
равна единице на тех наборах, на которых 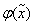 равна нулю, то СДНФ для
равна нулю, то СДНФ для 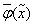 можно записать следующим образом:
можно записать следующим образом:
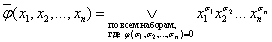
(2.11)
Найдем инверсию правой и левой части выражения (2.11):

Применяя дважды к полученному выражению правила де Моргана, получаем:
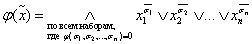
Последнее выражение и является СКНФ. Так как СКНФ получена из СДНФ, которая является единственным представлением для любой переключательной функции, то теорема доказана.
Пример 2.1.
Построить СДНФ и СКНФ для функции, заданной таблицей:
Таблица 2.6
| x1 |
x2 |
x3 |
φ( x1, x2, x3) |
0
0
0
0
1
1
1
1 |
0
0
1
1
0
0
1
1 |
0
1
0
1
0
1
0
1 |
1
0
1
0
0
1
1
0 |
|
Для построения СДНФ выпишем все наборы, на которых функция равна 1: 000, 010, 101, 110. Для каждого набора построим элементарную конъюнкцию, равную единице на этом наборе:
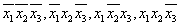
Соединяя эти конъюнкции знаками дизъюнкции, получаем СДНФ заданной функции:

Для построения СКНФ выписываем все наборы, на которых функция равна нулю: 001, 011, 100, 111. Для каждого набора построим элементарную дизъюнкцию, равную нулю на этом наборе:
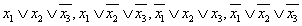
Объединяя с помощью конъюнкции все элементарные дизъюнкции, получаем КСНФ заданной функции:
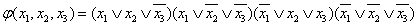
В заключении отметим, что совершенные нормальные формы не являются самым простым способом задания переключательных функций. Как правило, они допускают преобразование с помощью правил булевой алгебры к более простому виду. Способам построения простейших представлений переключательных функций посвящен один из следующих разделов курса.




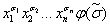 всегда равна нулю независимо от значений элементарной конъюнкции. Следовательно, такие члены из правой части выражения (2.4) можно удалить, поскольку они не влияют на результат дизъюнкции. Если же
всегда равна нулю независимо от значений элементарной конъюнкции. Следовательно, такие члены из правой части выражения (2.4) можно удалить, поскольку они не влияют на результат дизъюнкции. Если же 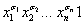 .
Учитывая сказанное СДНФ, можно записать в следующем виде:
.
Учитывая сказанное СДНФ, можно записать в следующем виде: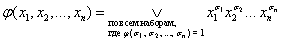
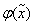 можно представить в виде СДНФ.
Для этого покажем, что значение функции
можно представить в виде СДНФ.
Для этого покажем, что значение функции 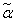 , что φ(α) = 0. При этом все элементарные конъюнкции в правой части выражения (2.10) равны нулю, так как ни один
набор
, что φ(α) = 0. При этом все элементарные конъюнкции в правой части выражения (2.10) равны нулю, так как ни один
набор  такой, что
такой, что 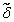 такой, что
такой, что 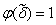 . В этом случае в правой части (2.10) найдется одна конъюнкция, у которой
. В этом случае в правой части (2.10) найдется одна конъюнкция, у которой 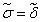 . Значение этой конъюнкции на наборе
. Значение этой конъюнкции на наборе 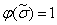 , соответствует единственная элементарная конъюнкция. Следовательно, совокупности наборов, на которых функция равна единице, соответствует единственная совокупность элементарных конъюнкций, являющаяся СДНФ заданной функции.
, соответствует единственная элементарная конъюнкция. Следовательно, совокупности наборов, на которых функция равна единице, соответствует единственная совокупность элементарных конъюнкций, являющаяся СДНФ заданной функции.
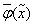 равна единице на тех наборах, на которых
равна единице на тех наборах, на которых