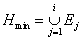Рассмотрим построение минимальных покрытий для таких функций, у которых в множестве Р имеются экстремали. Построение начинается с выделения множества экстремалей Е. Затем совокупность экстремалей следует удалить из множества Р, поскольку она должна входить в любое минимальное покрытие. Исключение экстремалей уменьшает число элементов множества Р и тем самым упрощает задачу построения минимального покрытия.
Каждая экстремаль покрывает некоторую совокупность наборов из Cn(φ). Если такие наборы являются существенными, то они не покрываются другими кодами из Р и их можно исключить из дальнейшего рассмотрения. Если же наборы, покрываемые экстремалями, не являются существенными, то их также целесообразно не учитывать в процессе дальнейшего построения, поскольку вполне достаточно, чтобы каждый набор из Cn(φ) покрывался хотя бы одним кодом искомого покрытия. Исключение таких наборов еще больше упрощает задачу построения минимального покрытия.
Практически исключение наборов, покрываемых экстремалями, можно выполнить, используя таблицу
покрытий. Столбцы такой таблицы отмечаются наборами 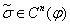 , на которых функция принимает значения единицы, а строки- кодами τ ∈ P, соответствующими минималям. Последовательно просматриваются все столбцы таблицы и на пересечении k-го столбца и l-й строки ставится отметка, если набор
, на которых функция принимает значения единицы, а строки- кодами τ ∈ P, соответствующими минималям. Последовательно просматриваются все столбцы таблицы и на пересечении k-го столбца и l-й строки ставится отметка, если набор  , которым отмечен столбец, покрывается минималью τ, которой отмечена строка.
В качестве отметки может быть использована, например, галочка. Таблицу покрытий используют, в первую очередь, для выделения экстремалей.
Если в некотором столбце таблицы имеется только одна отметка, то минималь, отмечающая эту строку, является экстремалью.
, которым отмечен столбец, покрывается минималью τ, которой отмечена строка.
В качестве отметки может быть использована, например, галочка. Таблицу покрытий используют, в первую очередь, для выделения экстремалей.
Если в некотором столбце таблицы имеется только одна отметка, то минималь, отмечающая эту строку, является экстремалью.
Например, табл. 3.2, которая построена для множества наборов
C1 = Cn(φ) = {0000, 0001, 1000, 0011, 0101, 0111, 1100, 1101}
и множества минималей P1 = {0zz1, 110z, 1z00, z101, z000, 000z},
Таблица 3.2
|
Pi
|

|
|
0000
|
0001
|
1000
|
0011
|
0101
|
0111
|
1100
|
1101
|
|
0zz1
|
|
∨
|
|
∨
|
∨
|
∨
|
|
|
|
110z
|
|
|
|
|
|
|
∨
|
∨
|
|
1z00
|
|
|
∨
|
|
|
|
∨
|
|
|
z101
|
|
|
|
|
∨
|
|
|
∨
|
|
z000
|
∨
|
|
∨
|
|
|
|
|
|
|
000z
|
∨
|
∨
|
|
|
|
|
|
|
|
представляющих функцию из примера 3.2, является таблицей покрытия. Из таблицы видно, что столбцы, отмеченные кодами 0011 и 0111, имеют только по одной отметке. Следовательно, эти коды являются существенными, а минималь 0zz1 является экстремалью. В правильности сделанного вывода можно убедиться, рассматривая геометрическое представление на рис. 8.27. Вершины 0011 и 0111 на этом рисунке покрываются только одной боковой гранью трехмерного куба, отмеченной кодом 0zz1. Таким образом, E1 = { 0zz1}.
Учитывая, что экстремали должны входить в любое минимальное покрытие, удалим из табл. 3.2 строку, соответствующую экстремали, и столбцы, соответствующие наборам Q1 = {0001, 0101, 0011, 0111}, покрываемым этой экстремалью. В результате получаем табл. 3.3, в которой представлено множество наборов,не покрываемых экстремалями : C2 = C1 \ Q1 = {0000, 1000, 1100, 1101} и множество минималей P2' = P1 \ E1 = {110z, 1z00, z101, z000, 000z}.
Таблица 3.3
|
Pi
|

|
|
0000
|
1000
|
1100
|
1101
|
|
110z
|
|
|
∨
|
∨
|
|
1z00
|
∨
|
∨
|
|
|
|
z101
|
|
|
|
∨
|
|
z000
|
∨
|
∨
|
|
|
|
000z
|
∨
|
|
|
|
|
Этой таблице соответствует геометрическое представление, приведенное на рис. 8.28.
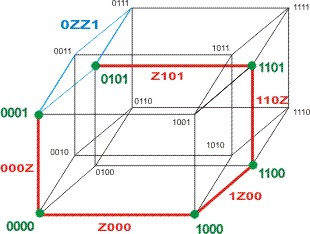
Рис.8.28
Для того чтобы формально описать рассмотренную ситуацию, обозначим множество наборов, покрываемых кодом h в множестве С2, как V(h1, C2) и введем отношение порядка между кодами множества Р2'. Если коды h1, h2 ∈ Р2' и выполняются два следующих условия:
- ранг кода h1 не меньше, чем ранг кода h2: r(h1) ≥ r(h2);
- все наборы, покрываемые кодом h1 в Р2', покрываются кодом h2: V(h1, C2) ⊆ V(h2, C2),
то между этими кодами существует отношение порядка, которое записывается так: h1 < h2.
Если же r(h1) = r(h2) и V(h1, C2) = V(h2, C2) то отношение порядка между кодами устанавливается произвольно. Например, меньшим кодом считают тот код, который раньше встречается в множестве P2'. Условимся называть меньшие коды в множестве P2' ущербными кодами.
Связь ущербных кодов с минимальными покрытиями устанавливается следующей теоремой.
| Теорема 3.4. |
Если коды h1, h2 ∈ Р2' и h1 < h2, то существует покрытие минимального ранга, не содержащее кода h1. |
Доказательство.
Предположим, что покрытие Н является минимальным и h1 ∈ Н. Поскольку h1 < h2, то согласно определению, h2 покрывает все наборы, покрываемые кодом h1 в множестве С2.
Заменим h1 в покрытии Н кодом h2. При этом ранг нового покрытия Н' не увеличивается, так как r(h1) ≥ r(h2), что и доказывает теорему.
Согласно последней теореме множество ущербных кодов P2'' можно исключить из P2' и решать задачу построения минимального покрытия для множества меньшего размера P2 = P2' \ P2''.
Возвращаясь к нашему примеру и анализируя табл. 3.3 и рис. 8.28, находим, что минимали 000z и z101 покрывают в множестве С2 по одному набору, соответственно 0000 и 1101, причем эти наборы покрываются также кодами z000 и 110z. Учитывая, что ранги всех рассматриваемых минималей одинаковы, приходим к заключению, что минимали 000z и z101 являются ущербными кодами. В результате удаления множества ущербных кодов P2'' = {000z, z101} из множества P2' получаем: P2 = P2' \ P2''.
Таблица 3.4
|
Pi
|

|
|
0000
|
1000
|
1100
|
1101
|
|
110z
|
|
|
∨
|
∨
|
|
1z00
|
|
∨
|
∨
|
|
|
z000
|
∨
|
∨
|
|
|
После удаления ущербных кодов из табл. 3.3 получаем табл. 3.4. Геометрическое представление, соответствующее этой таблице, приведено на рис. 8.29. В полученной таблице появились коды 0000 и 1101, покрываемые только одной минималью из Р2. Назовем эти наборы существенными наборами второго порядка, а коды, покрывающие их, - экстремалями второго порядка. Для выделения таких экстремалей естественно использовать прием, рассмотренный ранее. В результате получаем множество экстремалей второго порядка : Е2 = {110z, z000}. Это множество экстремалей покрывает все наборы множества С2, поэтому покрытие, включающее множество экстремалей первого и второго порядков, является искомым покрытием минимального ранга: Нmin = {0zz1, 110z, z000}. Геометрическое представление этого покрытия отражено на рис. 8.30. Для функций, зависящих от большого числа переменных, процедура упорядочения кодов и выделения экстремалей может повторяться несколько раз при построении минимального покрытия. Последовательность действий, выполняемая при таком построении, называется алгоритмом извлечения экстремалей и может быть представлена следующим образом.
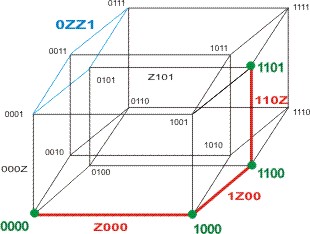
Рис.8.29
Дано множество минималей Р и исходное покрытие Q.
- Положить Р = Р1, С1 = Cn(φ) и i := 1.
- Пользуясь алгоритмом выделения экстремалей, построить множество Ei.
- Если Ei =
 , то алгоритм заканчивает свою работу, в противном случае выполнять следующий пункт. , то алгоритм заканчивает свою работу, в противном случае выполнять следующий пункт.
- i := i + 1.
- Построить множество Сi путем извлечения из Сi-1 всех наборов, покрываемых экстремалями из Ei-1.
- Если Сi =
 , то алгоритм заканчивает свою работу, в противном случае выполнять следующий пункт. , то алгоритм заканчивает свою работу, в противном случае выполнять следующий пункт.
- Построить множество Pi' = Pi-1 \ Ei-1.
- Упорядочить коды в множестве Pi' и определить множество ущербных кодов Pi''.
- Построить множество Pi = Pi' \ Pi''. Перейти к п. 2.
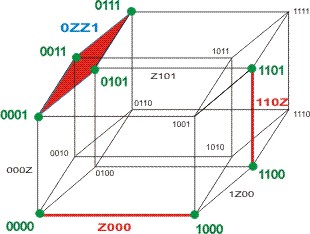
Рис.8.30
Приведенный алгоритм может закончить свою работу при выполнении п.3 или п.6. В первом случае окончание алгоритма означает, что экстремали
порядка i и более высоких порядков у заданной функции отсутствуют. Способ построения минимальных покрытий для функций, не имеющих экстремалей, будет рассмотрен в 8.3.6. Во втором случае окончание алгоритма показывает, что найдено минимальное покрытие, которое представляет собой совокупность экстремалей различных порядков:
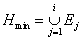




|
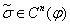 , на которых функция принимает значения единицы, а строки- кодами τ ∈ P, соответствующими минималям. Последовательно просматриваются все столбцы таблицы и на пересечении k-го столбца и l-й строки ставится отметка, если набор
, на которых функция принимает значения единицы, а строки- кодами τ ∈ P, соответствующими минималям. Последовательно просматриваются все столбцы таблицы и на пересечении k-го столбца и l-й строки ставится отметка, если набор  , которым отмечен столбец, покрывается минималью τ, которой отмечена строка.
В качестве отметки может быть использована, например, галочка. Таблицу покрытий используют, в первую очередь, для выделения экстремалей.
Если в некотором столбце таблицы имеется только одна отметка, то минималь, отмечающая эту строку, является экстремалью.
, которым отмечен столбец, покрывается минималью τ, которой отмечена строка.
В качестве отметки может быть использована, например, галочка. Таблицу покрытий используют, в первую очередь, для выделения экстремалей.
Если в некотором столбце таблицы имеется только одна отметка, то минималь, отмечающая эту строку, является экстремалью.