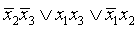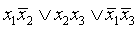
8.3.6. Построение минимальных покрытий для функций, не имеющих экстремалей

Множество минималей большинства переключательных функций, зависящих от многих переменных, не содержит экстремалей. Кроме того, совокупность минималей P_i, в которую не входит ни одна экстремаль, может получиться при выполнении i-го шага алгоритма извлечения. Совокупность минималей Р_i, не содержащую ни одной экстремали, назовем замкнутым множеством минималей.

Вначале рассмотрим способ построения минимальных покрытий замкнутых множеств для функций, заданных совокупностью двоичных наборов Cⁿ(φ). Этот способ заключается в том, что находятся все неизбыточные покрытия функции φ, затем определяется ранг каждого такого покрытия и, наконец, осуществляется выбор покрытия с наименьшим рангом.

Для построения всех неизбыточных покрытий воспользуемся таблицей покрытия.

Пример 3.4.

Построим таблицу покрытия функции φ, заданной совокупностью двоичных наборов Cⁿ(φ) = {000, 101, 100, 011, 010, 111}, множество минималей которой имеет вид P = {z00, 10z, 1z1, z11, 01z, 0z0}. В каждом столбце построенной табл. 3.5 имеется по две отметки. Это означает, что каждый двоичный набор покрывается двумя кодами из множества Р. Согласно определению, такое множество Р является замкнутым. В первом столбце таблицы расположены малые латинские буквы, используемые для сокращенного обозначения минималей или строк таблицы, которые они определяют.

Заметим, что по таблице покрытия нетрудно построить искомое покрытие. Для этого необходимо найти совокупность строк, которая имеет хотя бы одну отметку в каждом столбце, т. е. покрывает все двоичные наборы Cⁿ(φ). Например, совокупность строк H = {b, e, d, f} представляет собой покрытие. Однако построение некоторого, даже не избыточного покрытия, выбранного случайным образом по таблице, не гарантирует того, что найденное покрытие является покрытием минимального ранга.

Последовательность построения всех покрытий, определяемых таблицей, можно изобразить в виде дерева. Зафиксируем точку на плоскости, которую назовем корнем дерева. Число исходящих из корня дерева ребер возьмем равным числу отметок в первом столбце таблицы покрытия.

К концу каждого ребра прикрепим узел и отметим каждый такой узел буквой строки, имеющей отметку в первом столбце. Совокупность таких узлов образует первый ярус дерева. Число ребер, исходящих из каждого узла первого яруса, примем равным числу отметок во втором столбце таблицы. К концу каждого такого ребра прикрепим узел. Совокупность таких узлов образует второй ярус дерева. Каждое подмножество узлов второго яруса, достижимых из одного узла первого яруса, обозначим буквами строк, имеющих отметки во втором столбце. Продолжая построение описанным способом для всех остальных столбцов, получаем дерево, соответствующее таблице покрытий. Число ярусов такого дерева равно числу столбцов заданной таблицы. Каждый путь построенного дерева определяет совокупность строк, которая покрывает все столбцы таблицы. Следует отметить, что множество покрытий, соответствующее множеству путей такого дерева, содержит большое число повторяющихся и избыточных покрытий.

Определение всех путей дерева и соответствующего множества покрытий может быть выполнено алгебраически (метод Петрика), поскольку построение каждого яруса дерева производится независимо от других ярусов. Поставим в соответствие каждому столбцу таблицы дизъюнкцию букв, отмечающих те строки, которые имеют отметки в рассматриваемом столбце. Затем соединим все эти дизъюнкции знаками конъюнкции или умножения. Полученное выражение называется алгебраическим представлением таблицы покрытия. Если в этом выражении раскрыть скобки, то в результате получим столько произведений, сколько различных путей в дереве, соответствующем таблице покрытия.

При работе с алгебраическим представлением таблицы, покрытия оказывается возможным сформулировать правила преобразования таких представлений, которые облегчают построение множества неизбыточных покрытий. Если в покрытие, полученное в результате раскрытия скобок, входит произведение одинаковых букв αα, то это означает, что строка α покрывает два столбца таблицы, и поэтому справедливо равенство:

Покрытие α ∨ αβ, полученное из алгебраического представления таблицы, показывает, что в ней есть два столбца, которые покрываются строкой α или совокупностью строк α и β. При этом совокупность строк α и β является избыточной. Приведенные рассуждения показывают справедливость следующего равенства:

Используя равенства (3.1) и (3.2), нетрудно показать справедливость еще одного равенства:

Применение правил (3.1) - (3.3) позволяет исключить из алгебраического представления таблицы все повторяющиеся и неизбыточные покрытия. В качестве иллюстрации описанного способа рассмотрим пример.

Пример 3.5.

Найти все неизбыточные покрытия табл. 3.5. Алгебраическое представление заданной таблицы имеет вид

Применяя равенство (3.3), получаем

Отсюда, раскрывая скобки, находим произведения строк, определяющие неизбыточные покрытия:

В полученном множестве неизбыточных покрытий содержатся два минимальных покрытия: Q_min' = {a, c, e} и Q_min'' = {b, d, f}.

На практике построение всех неизбыточных покрытий возможно только для функций, зависящих от 3 - 7 переменных. У функций, зависящих от большого числа переменных, количество неизбыточных покрытий оказывается столь большим, что задача построения всех покрытий становится трудно разрешимой даже с помощью ЭВМ. Последнее обстоятельство приводит к тому, что при решении практических задач отказываются от построения минимального покрытия, а используют одно из неизбыточных покрытий. В некоторых случаях строят несколько неизбыточных покрытий и выбирают из них покрытие с меньшим рангом.

Задача построения некоторого неизбыточного покрытия функции, заданной совокупностью кодов Q и имеющей замкнутое множество минималей Р, может быть решена с использованием алгоритма извлечения экстремалей. Выберем произвольным образом некоторый код p_i ∈ P и построим покрытие Н', которое содержит код p_i. При этом мы можем действовать так, как если бы код p_i был экстремалью. Исключим из покрытия Q все наборы, покрываемые кодом p_i, тогда в множестве { P \ p_i } могут появиться ущербные коды и экстремали высших порядков, которые имеет смысл искать с помощью уже известного алгоритма извлечения. В результате выполнения этого алгоритма может быть получено либо неизбыточное покрытие, либо замкнутое множество минималей Р_i. Во втором случае необходимо повторить выбор еще одного кода, принудительным образом включаемого в искомое покрытие.

Приведенная процедура поиска неизбыточного покрытия основана на построении покрытия, обязательно содержащего выбранный код p_i. Нетрудно заметить, что эта же процедура может быть использована и для построения покрытия, не содержащего выбранный код p_i. Для этого достаточно удалить код p_i из множества минималей Р. При этом в множестве { P \ p_i } могут появиться экстремали, которые нетрудно получить с помощью алгоритма извлечения.

Описанные процедуры построения неизбыточных покрытий называются способом ветвления. Приведем пример построения покрытий способом ветвления.

Пример 3.6.

Построить неизбыточное покрытие функции, приведенной в примере 3.4. Выберем в качестве начального кода f. Тогда, полагая, что E₁ = {f}, после удаления наборов, покрываемых кодом f, получаем сокращенную таблицу покрытия (табл.3.6).

Из таблицы видно, что a < b и e < d. После удаления ущербных кодов получаем множество Р₂, в котором имеются коды b и d, являющиеся экстремалями. Поскольку экстремали покрывают все столбцы табл. 3.6, то окончательно имеем Q₁ = E₁ ∪ E₂ = {b, d, f}. Рассмотрим построение покрытия, не содержащего кода f. После удаления кода f из табл. 3.5 оказывается, что коды “а” и “е” становятся экстремалями. Извлекая экстремали и удаляя из множества Р₂ ущербные коды, получаем Q₂ = E₁ ∪ E₂ = {а, с, е}. Интересно отметить, что обе найденные совокупности кодов представляют собой минимальные покрытия заданной функции. Пользуясь кодами минималей, входящих в покрытия Q₁ и Q₂, нетрудно написать минимальные дизъюнктивные нормальные формы, соответствующие этим покрытиям:

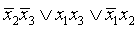и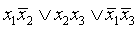

В заключение отметим, что метод ветвления позволяет получать в общем случае различные неизбыточные покрытия за счет выбора разных начальных кодов.

Пред.Страница  След.Страница    Раздел    Содержание