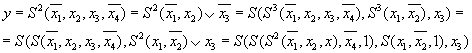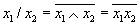
Пред.Страница  След.Страница  Раздел  Содержание

8.4.3. РЕАЛИЗАЦИЯ ФУНКЦИЙ В УНИВЕРСАЛЬНЫХ БАЗИСАХ



Логические или комбинационные схемы, являющиеся основой для построения различных вычислительных устройств и компьютеров, обычно строят из логических элементов (ЛЭ), каждый из которых реализует определенную переключательную функцию. При изготовлении ЛЭ, а также при построении БИС выгодно иметь один тип элементов, которые могут быть использованы для построения любой логической схемы. Такой логический элемент должен быть универсальным. Он должен обеспечивать возможность построения схемы для любой переключательной функции.

Подобные ЛЭ, как правило, реализуют переключательные функции, зависящие от небольшого числа аргументов (2-8), поэтому при построении логических схем, описываемых сложными переключательными функциями, приходится использовать суперпозицию переключательных функций, реализуемых ЛЭ. В логической схеме суперпозиции функций соответствует каскадное соединение ЛЭ.

Для упрощения перехода от переключательной функции к реализующей ее логической схеме переключательную функцию удобно записывать в так называемой операторной форме, в которой каждый использованный оператор F(x1,...,xk) реализует функцию φ(x1,...,xk) и однозначно соответствует некоторому ЛЭ с входами и одним выходом в логической схеме.



Определение: Базис называется универсальным, если позволяет построить для любой функции формулу, используя операцию только одного типа. Cоответственно, для любой функции в этом случае можно построить схему, используя элементы только одного типа.


8.4.3.1. Построение логических схем из элементов Шеффера

В качестве первого универсального базиса рассмотрим базис В={/} – “Штрих Шеффера” (отрицание конъюнкции):



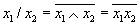
Для перехода к логическойсхеме введем оператор S(x1, x2) = x1 / x2, которому соответствует универсальный элемент Шеффера (рис. 8.36),где “↔“ – символ соответствия:


S(x1, x2)   ↔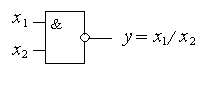  


Рис.8.36

Рассмотрим свойства операции "/".

  1. Операция не идемпотентна, так как
  2. Операция коммутативна, так как
  3. Операция не ассоциативна, так как

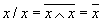
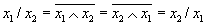
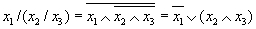
Доказательство.
Приведем к ДНФ обе части равенства:





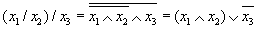
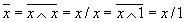
Полученные в результате преобразований формулы не эквивалентны, что доказывает неассоциативность операции "Штрих Шеффера".

Выразим теперь функции базиса 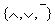через функцию " / ".

Инверсия: 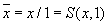. В дальнейшем будем использовать второй из рассмотренных способов инвертирования, заменяя все неиспользуемые аргументы константой 1.

Перейдем теперь к операторному представлению и построим соответствующие фрагменты логических схем для исходного базиса и базиса Шеффера ( рис. 8.37 ):







Рис.8.37


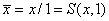
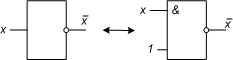
Конъюнкция:.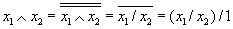

Перейдем теперь к операторному представлению и построим соответствующие фрагменты логических схем для исходного базиса и базиса Шеффера (рис. 8.38):







Рис.8.38

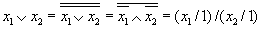
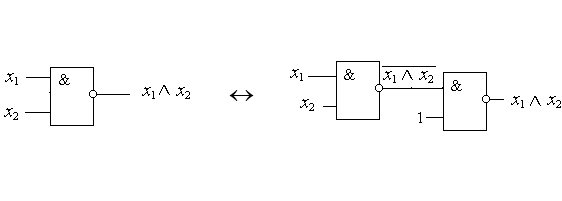
Примечание.
S3(x1, x2) = S(S2(x1, x2),1) = S(x1, x2).

Аналогично можно определить оператор произвольной степени:


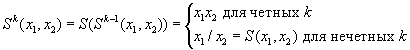
Дизъюнкция:



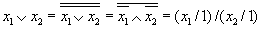
Перейдем теперь к операторному представлению и построим соответствующие фрагменты логических схем для исходного базиса и базиса Шеффера(рис.8.39).

x1 ∨ x2 = (x1 / 1)(x2 / 1) = S(S(x1,1),S(x2,1))





Рис.8.39

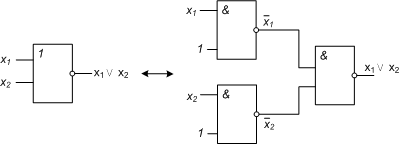
По аналогии с операциями конъюнкции и дизъюнкции можно рассматривать как обобщение двуместнойоперации "/" многоместную операцию "Штрих Шеффера" и многоместный оператор Шеффера:



где t – местность оператора и соответственно число входов многовходового универсального логического элемента Шеффера. Следует, однако,соблюдатьосторожностьприпопыткепредставить многоместнуюоперацию "Штрих Шеффера" в виде суперпозиции операций Шеффера меньшей местности. Следует помнить, что операция "/" не ассоциативна, поэтому, например, не справедливы равенства:

x1 / x2 / x3 = x1 / (x2 / x3) = (x1 / x2) / x3.

Эквивалентное преобразование имеет вид:



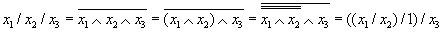
В операторной форме это преобразование имеет вид:

S(x1,x2,x3) = S(S2(x1,x2),x3) = S(x1,S2(x2,x3)).

и может быть проиллюстрировано фрагментами логических схем(рис. 8.40):





Рис.8.40

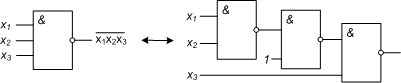
Рассмотрим два способа построения формул над базисом {/}, перехода к операторному представлению и построению логических схем.
Примем два допущения:

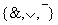Способ 1.
ШАГ 1. Произвольную формулу с помощью эквивалентных преобразований по законам булевой алгебры вначале привести к ДНФ. Затем к ДНФ применять закон двойного отрицания и закон де Моргана для перехода в базис Шеффера:



ШАГ 2. Если какие-либо операции Шеффера 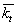(отрицание конъюнкции) в полученной записи имеют местность больше t, необходимо выразить их через операции местности. Операции с местностью меньше t следует привести к необходимой местности, заменяя отсутствующие переменные константой 1.

ШАГ 3. Заменить каждую операцию Шеффера местностью t соответствующим оператором Шеффера, построить логическую схему.

Примечание:
Вырожденной (однобуквенной) конъюнкции вида 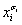в ДНФ вновой формуле соответствует вырожденная (однобуквенная) операция Шеффера вида .


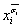Пример 4.1.
Пусть исходной является формула в ДНФ.

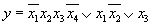и t = 3



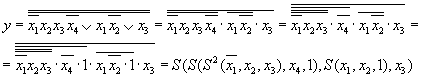
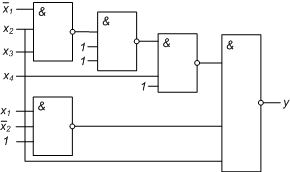
По операторному представлению легко построить логическую схему (рис 8.41 ).





Рис.8.41

Способ 2.
Произвольная формула над базисом 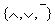приводится к новому виду последовательной заменой операций исходного базиса эквивалентными подформулами в новом базисе в операторной форме. После этого понижаются степени операторов 3 и выше.

Примечание:
Вначале следует использовать операторы Шеффера произвольной местности, а затем привести их к необходимому значению t.


Пример 4.2.
Пусть исходной является формула в ДНФ.

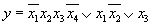и t = 3



Соответствующая логическая схема аналогична приведенной на рис. 8.41.



Пред.Страница  След.Страница    Раздел    Содержание