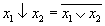8.4.3.2. Построение логических схем из элементов Пирса

В качестве второго универсального базиса рассмотрим базис {↓} - "Стрелка Пирса" (отрицание дизъюнкции): .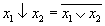

Для перехода к логической схеме введем оператор Р(x₁,x₂) = x₁ ↓ x₂, которому соответствует универсальный элемент Пирса ( рис.8.42 ):

Рис.8.42

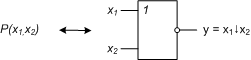
Рассмотрим свойства операции "↓".

1. Операция не идемпотентна, так как


2. Операция коммутативна, так как


3. Операция не ассоциативна, так как x₁ ↓(x₂ ↓ x₃) ≠ (x₁ ↓ x₂) ↓ x₃.

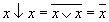
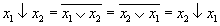
Доказательство.
Приведем к КНФ обе части равенства

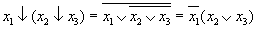
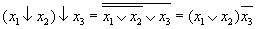
Выразим теперь функции базиса 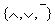через функцию "↓". Инверсия: 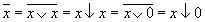. В дальнейшем будем использовать второй из рассмотренных способов инвертирования, заменяя все неиспользуемые аргументы константой 0.

Перейдем теперь к операторному представлению и построим соответствующие фрагменты логических схем для исходного базиса и базиса Пирса (рис. 8.43 ).

Рис.8.43

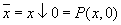
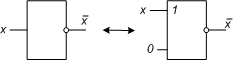
Дизъюнкция: .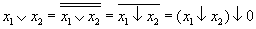

Перейдем теперь к операторному представлению и построим соответствующие фрагменты логических схем для исходного базиса и базиса Пирса (рис.8.44 ):

Рис.8.44

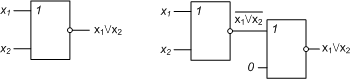
Примечание:
P³(x₁,x₂) = P(P²(x₁,x₂),0) = P(x₁,x₂).

Аналогично можно определить оператор произвольной степени:

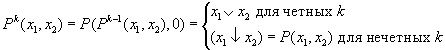
Конъюнкция: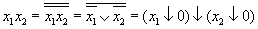

Перейдем теперь к операторному представлению и построим соответствующие фрагменты логических схем для исходного базиса и базиса Пирса (рис. 8.45 ):

Рис.8.45

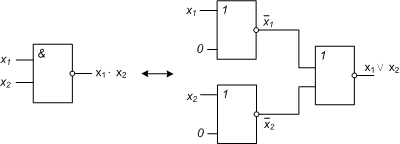
По аналогии с операциями ∧ и ∨ можно рассматривать как обобщение двуместной операции "↓" многоместную операцию "Стрелка Пирса" и многоместный оператор Пирса: 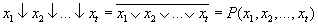, где t – местность оператора и соответственно число входов многовходового универсального логического элемента Пирса.

Следует, однако, соблюдать осторожность при попытке представить многоместную операцию "Стрелка Пирса" в виде суперпозиции операций Пирса меньшей местности. Следует помнить, что операция "↓" не ассоциативна, поэтому, например, не справедливы равенства: x₁ ↓ x₂ ↓ x₃ = x₁ ↓ (x₂ ↓ x₃) = (x₁ ↓ x₂) ↓ x₃.

Эквивалентное преобразование имеет вид:

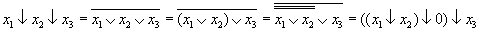
В операторной форме это имеет вид: P(x₁,x₂,x₃) = P(P²(x₁,x₂),x₃) = P(x₁,P²(x₂,x₃)) и может быть проиллюстрировано фрагментами логических схем (рис.8.46):

Рис.8.46

Рассмотрим два способа построения формул над базисом {↓}, перехода к операторному представлению и построению логических схем. Примем допущения:

• исходной формулой является произвольная формула над базисом ;
• местность оператора Пирса и соответственно число входов универсального логического элемента Пирса фиксирована (t =const);
• допускаются инверсии элементарных переменных.

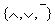Способ 1.
ШАГ 1. Произвольная формула с помощью эквивалентных преобразований по законам булевой алгебры вначале приводится к КНФ. Затем к КНФ применяется закон двойного отрицания и закон де Моргана для перехода в базис Пирса:

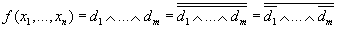
ШАГ 2. Если какие – либо операции Пирса 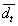(отрицание дизъюнкции ) в полученной записи имеют местность больше t, необходимо выразить их через операции местности t. Операции с местностью меньше t следует привести к необходимой местности, заменяя отсутствующие переменные константой 0.

ШАГ 3. Заменить каждую операцию Пирса местностью t соответствующим оператором Пирса, построить логическую схему.

Примечание:
Вырожденной (однобуквенной) дизъюнкции вида 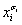в КНФ в новой формуле соответствует вырожденная (однобуквенная) операция Пирса вида .

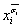Пример 4.3.
Пусть исходной является формула в КНФ.

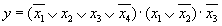и t = 3

Рис.8.47

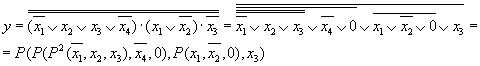
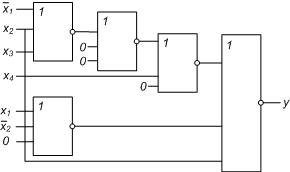
Способ 2.
Произвольная формула над базисом 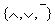приводится к новому виду последовательной заменой операций исходного базиса эквивалентными подформулами в новом базисе в операторной форме. После этого понижаются степени операторов степени 3 и выше.

Примечание:
Вначале следует использовать операторы Пирса произвольной местности, а затем привести их к необходимому значению t.

Пример 4.4.
Пусть исходной является формула в КНФ.

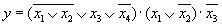и t = 3

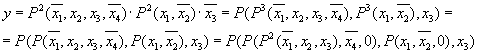
В заключение заметим, что замена в исходной формуле над базисом {/} ({↓}) символов операций /(↓) на ↓(/) и констант 1(0) на 0(1) дает формулу над базисом {↓}({/}) для инверсной функции.

Пред.Страница  След.Страница    Раздел    Содержание