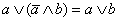8.1.2.2. Основные теоремы 2
| Теорема 1.8. |
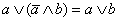(поглощение дополнения в ∧). |
Доказательство.
 |
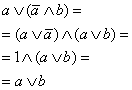∣А4б: дистрибутивность ∨ к ∧ ∣А6б: свойство дополнения в ∨ ∣А5а: свойство 1 в ∧ |
| Теорема 1.9. |
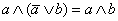(поглощение дополнения в ∨). |
Доказательство.
 |
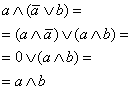∣А4а: дистрибутивность ∧ к ∨ ∣А6а: свойство дополнения в ∧ ∣А5б: свойство 0 в ∨ |
Теоремы 1.3 - 1.9 часто используются на практике для эквивалентных преобразований и упрощения булевских выражений. Применение теорем рассмотрим на нескольких примерах.
Пример 1.9.
Упростить выражение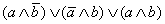 
.
 |
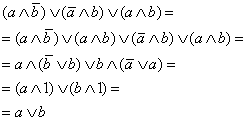∣А1б: идемпотентность ∨ ∣А4а: дистрибутивность∧ к ∨ ∣А6б:свойство дополнения в ∨ ∣А5а: свойство 1 в ∧ |
Пример 1.10.
Упростить выражение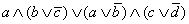 
.
 |
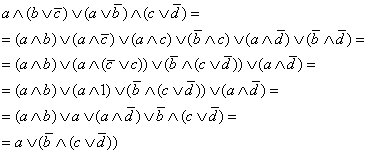∣А4а: дистрибутивность ∧ к ∨ ∣А4а: дистрибутивность ∧ к ∨ ∣А6б:свойство дополнения в ∨ ∣А5а: свойство 1 в ∧ ∣Т1.6:поглощение элемента в ∧ |
Следующие две теоремы носят название теорем де Моргана.
| Теорема 1.10. |
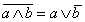(Теорема де Моргана для ∧). |
Доказательство.
Выражение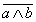 
является дополнением выражения (a ∧ b), поэтому согласно аксиомам А6 можно записать:
 |
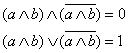∣А6a:свойство дополнения в ∧ ∣А6б: свойство дополнения в ∨ |
Если теорема справедлива, то,заменив в этих выражениях 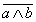на 
∨ 
,
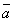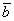мы также должны получить верные равенства:
 |
(**) (***) |
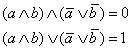Преобразуем вначале левую часть равенства (**):
 |
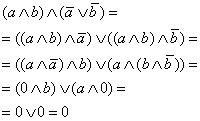∣А4а: дистрибутивность ∧ к ∨ ∣А3а: ассоциативность ∧ ∣А6а: свойство дополнения в ∧ ∣А5а: свойство 0 в ∧ ∣А1б: идемпотентность ∨ |
Преобразуем теперь левую часть равенства(***):
 |
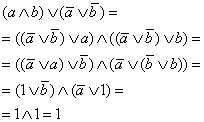∣А4б: дистрибутивность ∨ к ∧ ∣А3б: ассоциативность ∨ ∣А6б: свойство дополнения в ∨ ∣Т1.5: свойство 1 в ∨ ∣А1а: идемпотентность ∧ |
Из справедливости равенств (**) и (***) следует справедливость теоремы.