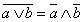8.1.2.3. Основные теоремы 3
| Теорема 1.11. |
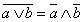(теорема де Моргана для ∨). |
Эта теорема доказывается аналогично предыдущей, поэтому провести ее доказательство рекомендуется самостоятельно.
Теоремы де Моргана часто используются на практике для отыскания дополнений булевых выражений, а также для их преобразования.
Пример 1.11.
Упростить следующее выражение булевой алгебры:
 |
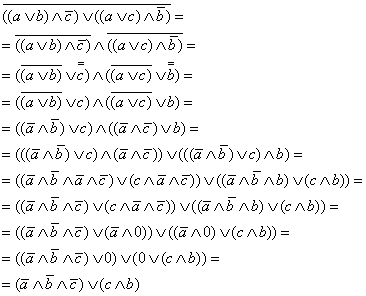∣Т1.11: теорема де Моргана для ∨ ∣Т1.10: теорема де Моргана для ∧ ∣Т1.3: закон двойного дополнения ∣Т1.11: теорема де Моргана для ∨ ∣А4а: дистрибутивность ∧ к ∨ ∣А4а: дистрибутивность ∧ к ∨ ∣A1а: идемпотентность ∧ ∣A6а:свойство обратного элемента в ∧ ∣Т1.4: свойство 0 в ∧ ∣A5б: свойство 0 в ∨ |
На основании теорем де Моргана можно сформулировать простое правило для приведения дополнения булевого выражения к виду, не содержащему знаков ∧ и ∨ под символом операции дополнения.
Для построения дополнения выражения булевой алгебры достаточно заменить в нем все символы ∧ на символы ∨, все символы ∨ на символы ∧, все символы элементов решетки - на их дополнения, после чего применить закон двойного дополнения.
Пример 1.12.
Согласно приведенному правилу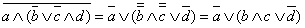 
.
Если часть преобразуемого выражения, содержащая символы ∧ и ∨, находится под знаком дополнения, то при построении дополнения символ дополнения над частью выражения нужно отбросить, а выражение, стоящее под ним, оставить без изменения.
Пример 1.13.
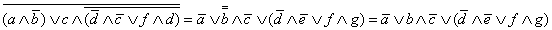
| Теорема 1.12. |
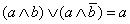(склеивание конъюнкций). |
Доказательство.
 |
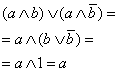∣А4а: дистрибутивность ∧ к ∨ ∣А6а: свойство дополнения в ∨ ∣А5б: свойство 1 в ∧ |
| Теорема 1.13. |
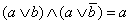(склеивание дизъюнкций). |
Доказательство.
 |
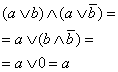∣А4а: дистрибутивность ∧ к ∨ ∣А6а: свойство дополнения в ∧ ∣А5б: свойство 0 в ∨ |
Пример 1.14.
Упростить выражение из примера 1.9.
 |
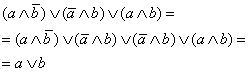∣А1б: идемпотентность ∨ ∣Т1.12:склеивание конъюнкций |
В предшествующем изложении основное внимание было сконцентрировано на рассмотрении свойств формальных алгебраических систем, поэтому во всех предыдущих определениях и доказательствах нигде не использовались свойства элементов множества B и правила выполнения основных операций. Однако, для различных по своей природе множеств и основных операций могут быть построены различные интерпретации булевой алгебры. Напомним, что бинарную операцию считают определенной на множестве A = {a,b,c,...}, если указаны правила, согласно которым каждым двум элементам a и b из множества A поставлен в соответствие некоторый элемент из A, который называется результатом операции.