Операции конъюнкции и дизъюнкции определим как известные операции пересечения и объединения множеств. Эти операции идемпотентны, коммутативны и ассоциативны, для них выполняются законы дистрибутивности (аксиомы А1 - А4).
8.1.2.4. Алгебра подмножеств
В качестве первого примера рассмотрим множество всех подмножеств непустого
конечного множества М. Для простоты примем, что М состоит
из трех элементов М = {u, ν, ω}. Тогда множество
всех подмножеств М (степень множества М) имеет вид:
![]() , {u}, {ν}, {ω}, {u, ν}, {u, ω}, {ν, ω}, {u, ν, ω}}.
, {u}, {ν}, {ω}, {u, ν}, {u, ω}, {ν, ω}, {u, ν, ω}}.
Операции конъюнкции и дизъюнкции определим как известные операции пересечения и объединения
множеств. Эти операции идемпотентны, коммутативны и ассоциативны, для них
выполняются законы дистрибутивности (аксиомы А1 - А4).
Элементом 0 в рассматриваемом случае является пустое множество ![]() , а элементом
1 - множество М. При этом для любого подмножества m ∈ P
выполняются аксиомы А5а и А5б:
, а элементом
1 - множество М. При этом для любого подмножества m ∈ P
выполняются аксиомы А5а и А5б:
m ∪ ![]() = m
= m
поскольку любой элемент P является подмножеством М.
Операцию дополнения определим следующим образом. Результатом дополнения подмножества m ∈ P является множество элементов М, не входящих в подмножество m. Например,
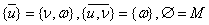
Из определения дополнения следует, что для любого подмножества m ∈ P выполняются аксиомы А6а и А6б:
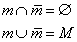
Таким образом, множество P и операции пересечения, объединения, дополнения образуют булеву алгебру множества всех подмножеств множества М, в которой справедливы все введенные ранее аксиомы. Справедливость теорем в рассматриваемой алгебре рекомендуется проверить самостоятельно.