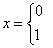8.1.2.5. Алгебра контактных схем
В качестве второго примера рассмотрим алгебру контактных схем, которая представляет собой одну из интерпретаций алгебры Буля.
Следуя К. Шеннону, обозначим проводимость короткозамкнутой цепи символом 1, а проводимость
цепи, состоящей из несвязанных друг с другом полюсов А и В
- символом 0 (рис. 8.9.а). Проводимость цепи, изображенной на рис. 8.9.б,
зависит от состояния контакта, включенного между полюсами А и В
и управляемого переменной x:
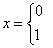
(контакт разомкнут)
(контакт замкнут)
Тогда проводимость цепи между полюсами А и В можно описать выражением:
Обозначим последовательное соединение контактов символом операции конъюнкции или точкой, которую в дальнейшем, как и знак умножения в обычной алгебре, можно опускать, а параллельное соединение контактов - символом операции дизъюнкции ∨, как это показано на рис.8.9, в. На этом же рисунке приведены таблицы, в которых для каждой комбинации значений переменных указаны результаты операций конъюнкции ∧ и дизъюнкции ∨.
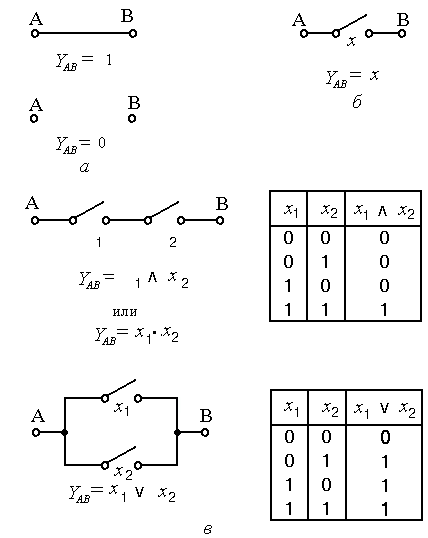
Элементарные познания в электротехнике позволят без труда убедиться в справедливости аксиом А1 (идемпотентность), А2 (коммутативность), А3 (ассоциативность) для операций конъюнкции ∧ и дизъюнкции ∨ в вырожденной булевой алгебре.
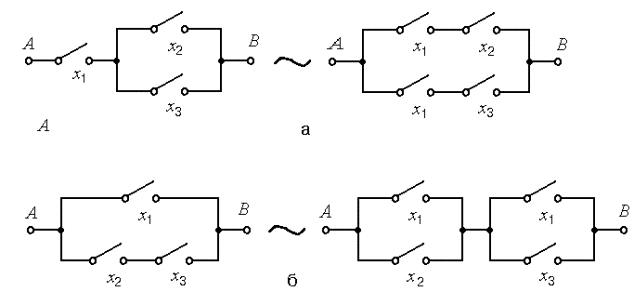
Нетрудно также убедиться в справедливости в алгебре контактных схем аксиом дистрибутивности А4. На рис. 8.10 (а), показано эквивалентное преобразование контактных схем, подтверждающее справедливость аксиомы А4а: x1 ∧ (x2 ∨ x3) = (x1 ∧ x2) ∨ (x1 ∧ x3). Справедливость аксиомы А4б : x1 ∨ (x2 ∧ x3) = (x1 ∨ x2) ∧ (x1 ∨ x3) подтверждает рис. 8.10, б.
Роль единицы по отношению к операции конъюнкции ∧ играет элемент 1 ∈ В(2). Нетрудно убедиться в справедливости аксиомы А5а: x ∧ 1 = x, так как включение последовательно с контактом x короткозамкнутой цепи не влияет на проводимость цепи в целом. Соответственно, роль единицы по отношению к операции дизъюнкции ∨ играет элемент 0 ∈ В(2). Так как включение параллельно контакту тождественно разомкнутой цепи не влияет на проводимость цепи в целом, то это подтверждает справедливость аксиомы А5б: x ∨ 0 = x в алгебре контактных схем.
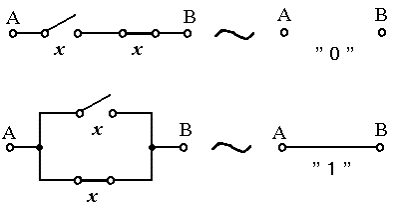
Обычно для построения схем используют два типа контактов, обозначаемых x
и 
,
таких, что контакт разомкнут, когда контакт x замкнут,
и наоборот, контакт замкнут, когда x разомкнут. Проводимость
контакта в такой паре всегда противоположна проводимости контакта x. Учитывая последнее обстоятельство, считают функцией переменной x и называют ее функцией инверсии или отрицания (рис. 8.11).
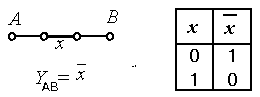
Функция инверсии (отрицания) соответствует операции дополнения в булевой алгебре. Рис. 8.12
иллюстрирует справедливость аксиом А6 валгебре контактных схем:
= 0,
А6б: x ∨ = 1.
Убедиться в справедливости теорем булевой алгебры применительно к релейно-контактным схемам читателю предлагается самостоятельно.
Пользуясь введенными обозначениями, можно получать алгебраические выражения переключательных функций, описывающие
работу последовательно-параллельных контактных схем. По этим формулам можно вычислять проводимость цепи при различных значениях проводимостей контактов, используя для определения результата каждой операции таблицы, приведенные
на рис. 8.9, 8.11. Если, применяя введенные операции для каждой последовательно-параллельной
схемы можно написать соответствующую ей формулу, то можно утверждать, что и наоборот, каждой формуле, содержащей операции конъюнкции, дизъюнкции и отрицания, соответствует последовательно-параллельная схема. Для того чтобы построить эту схему, каждому знаку дизъюнкции нужно поставить в соответствие параллельное соединение ветвей в схеме, а каждому знаку конъюнкции - последовательное.
Так, например, выражению:
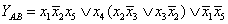
соответствует схема, приведенная на рис. 8.13.
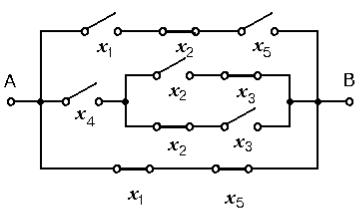
Возможность описания контактных схем с помощью формул является весьма ценной по двум причинам. Во-первых, по формулам гораздо удобнее проверить работу схемы, чем по рисунку. Во-вторых, выгода от использования формул заключается в том, что при задании условий работы схемы в виде формул процесс построения схемы, реализующей эти условия, становится весьма простым. Более того, оказывается, что существует ряд эквивалентных преобразований, в результате которых формулы приобретают более простой вид. Возможность упрощения формул, задающих условия работы схем, позволяет строить более простые схемы с меньшим числом контактов без трудоемкого анализа графического изображения схемы.
Работу логических элементов можно описывать с помощью формул, используемых в анализе контактных схем. Подобно последовательному и параллельному соединениям контактов можно построить логические элементы, реализующие операции конъюнкции и дизъюнкции. Согласно таблице конъюнкции (рис. 8.9, в) элемент, реализующий операцию конъюнкции, должен вырабатывать на выходе потенциал, соответствующий 1, только в том случае, когда оба входных потенциала соответствуют 1. Аналогично, элемент, реализующий дизъюнкцию, создает на выходе потенциал, соответствующий 1, если хотя бы на один вход подается сигнал, соответствующий 1. Символическое изображение основных логических элементов и реализуемые ими функции приведены на рис. 8.14.
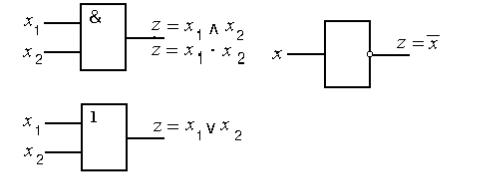
Схемы, построенные из логических элементов, называются логическими схемами. Работа логических
схем, так же, как и работа контактных схем, может быть описана с помощью
формул. Например переключательной функции
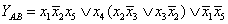
соответствует схема из логических элементов, изображенная на рис. 8.15.
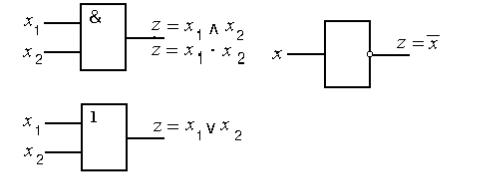
Общим свойствомлогических и контактных схем является то, что выходной сигнал схемы (проводимость цепи) в каждый момент времени определяется только комбинацией входных сигналов, действующих в рассматриваемый момент времени, и не зависит от сигналов, присутствовавших на входе в предшествующие моменты времени. Схемы, обладающие таким свойством, называют комбинационными.
Математический аппарат для описания работты и преобразования алгебраических выражений комбинационных схем в дальнейшем получил название алгебры переключательных функций, которая, в свою очередь, является частным случаем булевой алгебры.