|
ОЛИМПИАДНЫЕ И РЕЙТИНГОВЫЕ ЗАДАЧИ
по начертательной и компьютерной геометрии
(пособие к решению задач повышенной сложности. )
Р. А. Сакаев
1. Условия задач
2. Алгоритмы решения задач
2. Алгоритмы решения задач
Общая схема решения всех задач сводится к трем этапам:
- анализу данных;
- поиску идеи решения и ее записи;
- геометрическим построениям.
В анализе данных по заданным проекциям геометрических
объектов мысленно представляют их форму и взаимное
расположение в пространстве. Исходные проекции рекомендуется
выделить черным цветом, соблюдая типы и толщины линий
по правилам, установленным стандартами ЕСКД. Главное - понять условие задачи.
На этапе поиска идеи намечается «пространственный» план решения задачи, т.е.
последовательность геометрических операций, с помощью которых может быть получен
ответ на поставленную задачу. Поскольку способов решения, как правило, бывает
несколько, целесообразно выбрать из них наименее трудоемкий.
На последнем этапе осуществляется реализация на чертеже идеи решения методами
начертательной геометрии или с помощью специализированных прикладных программ.
Все вспомогательные построения и обозначения желательно выделить зеленым цветом,
а конечный результат - красным. Удалять вспомогательные построения
не рекомендуется.
Приводим идеи решений ко всем задачам.
Задача 1. Как
известно, расстояние между скрещивающимися прямыми
равно расстоянию между параллельными плоскостями, проведенными
через эти прямые. Так как в данной задаче а2||b2,
то указанные плоскости будут фронтально проецирующими.
Из произвольной точки В2 на прямой b опустим
перпендикуляр на проекцию а2 и проведем
из точки В1 горизонтальный отрезок,
являющийся горизонтальной проекцией фронтали. Теперь
осталось переместить этот отрезок параллельно самому
себе вдоль прямой b до касания с прямой а.
Задача 2. Прямая t должна принадлежать плоскости , проходящей через
середину отрезка АВ, и быть перпендикулярной ему. Любая линия, взятая
в плоскости , будет перпендикулярна отрезку АВ. Воспользуемся теоремой
о проецировании прямого угла. Через середину [АВ] проведем фронталь и горизонталь в плоскости . Отрезок А2В2 перпендикулярен
к фронтальной проекции фронтали. Отрезок А1В1 найдем
на перпендикуляре к горизонтальной проекции горизонтали.
Задача 3. Требуется построить плоскость, равноудаленную от двух прямых, а значит,
параллельную им. Проведем фронтально проецирующую прямую, пересекающую две
заданные. Отрезок этой прямой, заключенный между точками ее пересечения с заданными,
разделим пополам. Через середину этого отрезка проводим две линии, параллельные
заданным. Построенные две линии образуют искомую плоскость.
Задача 4. В произвольной точке пространства проводятся прямые, параллельные
заданным. На них откладываются произвольные отрезки равной длины. Их концы
будут вершинами треугольника, вписанного в основание кругового конуса с образующими
из построенных отрезков. Любые две прямые, проведенные через точку Т параллельно
пересекающимся сторонам треугольника, зададут искомую плоскость.
Задача 5. В произвольном месте чертежа построим треугольник, две стороны которого
равны и параллельны проекциям отрезков a2 и b2.
Третья сторона, замыкающая концы построенных отрезков, определит направление,
перпендикулярно которому необходимо построить искомую плоскость проекций. В
данной задаче исходные данные таковы, что замыкающая сторона - горизонталь. Таким образом, искомая плоскость проекций, на которую
заданные отрезки будут проецироваться как равные по модулю и параллельные по
направлению, окажется перпендикулярной к горизонтальной проекции этой горизонтали.
Задача 6. Следует преобразовать проекции так, чтобы одна из заданных трех прямых
проецировалась в точку. Тогда искомая прямая пройдет через произвольно взятую
точку любой из прямых общего положения и след проецирующей прямой. Задачу можно
решить и без преобразования чертежа, воспользовавшись темой о пересечении прямой
линии с плоскостью.
Задача 7. Проведем новую ось проекций х14, параллельную линии,
проходящей через центры шаров на плоскости П1. Наплоскости П4 построим
проекцию касающихся шаров и отметим искомую точку. Осталось найти исходные
проекции этой точки.
Задача 8. Задача сводится к определению высот пирамидок, ребрами которых являются
прямые, соединяющие центры шаров.
Задача 9. На плоскости проекций, перпендикулярной , строим проекцию В¢3,
симметричную В3 относительно 3. Отрезок A3B¢3 пересечет проекцию 3 в
искомой точке К3 отражения радиосигнала. По построению получится
равенство углов падения и отражения. Проекции К1 и К2 найдем
обратным проецированием.
Задача 10. Через прямую а проведем две фронтально проецирующие произвольно
взятые прямые. Перенесем их проекции на плоскости П1, П4 и
П5 и найдем две точки их пересечения с проекцией а5.
По этим двум точкам построим искомую проекцию а1.
Задача 11. Через центр О квадрата проведем горизонталь hиз условия h É[BD]. Вторая
диагональ А1С1 перпендикулярна h1 по
теореме о проецировании прямого угла. Отметив вершины А1С1,
с помощью преобразования чертежа найдем модуль /А01С01/.
На проекции h1 отложим /В1D1/
= /А01С01/.
Задача 12. Пусть в исходном положении отрезок АВ занимает профильно
проецирующее положение. Тогда /А01В01/
= /А02В02/ = m. Дважды применив
способ вращения, установим искомое положение растяжки АВ и 4 варианта
ее расположения в пространстве. Есть и другие способы решения задачи, например
с помощью темы о пересечении поверхностей двух конусов вращения.
Задача 13. Через середину отрезка ABи перпендикулярно ему проведем плоскость
общего положения = (f Ç h).
Согласно теореме о проецировании прямого угла имеем: h1 ^ A1B1 и f2 ^ A2B2. Осталось решить центральную
задачу начертательной геометрии: построить искомую точку пересечения прямой t и
плоскости.
Задача 14. Следует построить сферу с точками А и В на ее поверхности
и определить точки пересечения прямой t с поверхностью сферы.
Задача 15. Геометрическим местом точек, равноудаленных от середин A, B и C картин
и стола, является нормаль к DABC,
проведенная через центр описанной вокруг треугольника окружности. Искомая точка D находится
на пересечении этой нормали с горизонтальной плоскостью, проведенной на высоте h.
Задача 16. Найдем след прямой t на плоскости П1 и построим
сферу, касательную к плоскости П1, но с центром на этой прямой.
Далее через горизонтальную проекцию следа прямой проведем к сфере касательные
плоскости проекций П4 (два варианта решения), которые
и будут новыми осями проекций. Искомые фронтальные проекции t4,
определятся симметричным отображением t1 относительно этих
новых осей.
Задача 17. Через точку А и вершину S конуса проведем касательную
плоскость. Искомую точку С найдем на пересечении прямой с с касательной
плоскостью.
Задача 18. Искомые точки находятся на пересечении горизонтальной плоскости,
проходящей на высоте 10 км, с двумя сферами, радиусы которых для центров A и B соответственно
равны 20 и 14 км. Таким образом, задача сводится к пересечению двух окружностей,
лежащих в одной плоскости и являющихся параллелями сфер. Радиусы этих окружностей
замерим на фронтальной плоскости проекций, а две искомые точки найдем на горизонтальной.
Рекомендуемый масштаб чертежа 1:(2*105),
т.е. в 1 см - 2 км.
Задача 19. Проведем плоскость проекций П4 при П4 ^ D (f Ç h ). В ней - контур
тени, отрезок прямой, заключенный между крайними образующими конуса, касательными
к сфере планеты. Для построения контура тени на плоскости П1 воспользуемся
четырьмя опорными точками на концах малой и большой осей эллипса. Две построенные
проекции контура тени однозначно определяют и ее проекцию на плоскости П2.
Задача 20. Известно, что эллипс можно трактовать как сжатую окружность. Положение
искомого плоского сечения определится углом к горизонтальной оси, косинус которого
равен a/b. На горизонтальной плоскости проекций a и b- длины малой и большой осей основания конуса.
На фронтальной плоскости проекций искомое сечение будет проецирующим и измеряться
отрезком, равным по модулю диаметру окружности, описанной вокруг DABC. Взаимное положение этой окружности и сечения определят
положение искомой фронтально проецирующей оси. Количество решений - 2.
Задача 21. Строим плоскость проекций П4, перпендикулярную горизонталям a и b.
На поверхности цилиндра с радиусом m и с центром в точке а4 найдем
точку Е4 (над палубой) и затем точку Е2.
Проведем отрезок ЕК ^ t: (E1K1 ^ t1) Ù (K t). Способом вращения или иначе найдем модуль /ЕК/.
Задача 22. На плоскости проекций, перпендикулярной направлению t, проведем
вспомогательную плоскость через точку А и линию t. Плоскость
рассечет планету по окружности. На плоскости проекций,
параллельной секущей плоскости, окружность сечения проецируется без искажения.
Проведя касательные из точки А к этой окружности, получим две точки
их пересечения с линией t. Это искомые точки, ограничивающие невидимую
часть траектории.
Задача 23. Способом вращения повернем стержень а вокруг горизонтально
проецирующей прямой, проходящей через точку К. Тогда плоскость щита
займет проецирующее положение, образуя угол 60° с плоскостью П1. Начертив треугольник
щита в горизонтальной проекции, повернем его в исходное положение.
Задача 24. Строим плоскость проекций П4 ^ А1В1. Проводим
биссекторные плоскости в двугранном угле с общим ребром АВ и в двугранном
угле между DАВС и плоскостью
проекций П1. Положение центра сферы определят две построенные биссекторные
плоскости, которые на плоскости П4 занимают проецирующее
положение.
Задача 25. Проекции точки С движутся ^ А1В1 на
плоскости П1 и по эллипсу на плоскости П2. Малая ось
эллипса - горизонтальна, а большая - вертикальна.
Их размеры можно найти на плоскости П1.Искомые два решения для вершины С на
плоскости П2 определятся двумя точками пересечения эллипса с окружностью,
построенной на диаметре /А2В2/.
Задача 26. Все точки проще всего найти во вспомогательных горизонтальных плоскостях,
секущих тор по окружностям, а конус - по гиперболам. Пересечения этих окружностей
и гипербол определят положение искомых точек.
Задача 27. Из анализа данных следует, что диаметр окружности основания равен
длине образующей конуса. Значит, на фронтальной проекции эпюра Монжа конус
должен изображаться как равносторонний треугольник! Разделим боковую поверхность
развертки конуса на 6 равных частей и проведем по границам деления вспомогательные
образующие. Пять из них пересекут отрезок АВ в 5 точках. Отметив эти
точки, перенесем их на эпюр Монжа. Через точки А, В и 5 построенных
точек пройдет искомая кривая на поверхности конуса
Задача 28. Решение сводится к построению линии на поверхности по предварительно
найденным опорным и произвольным точкам. Отметим, что на передней грани пирамиды
малая ось эллипса должна быть горизонтальной, а большая - вертикальной.
Это весьма трудоемкая задача. Уменьшить эту трудоемкость позволит использование
трехмерной системы геометрического моделирования.
Задача 29. Искомый DАВС составляет половину равностороннего DАDС. Точка В во всех проекциях будет находиться
посредине отрезка АD. Значит, проекцию D1 найдем легко,
удвоив длину отрезка А1В1. Так как /А1D1/
= /D1С1/, то проекция С1 определится
в двух точках пересечения соответствующей дуги с линией проекционной связи.
Проведем отрезок х14 = /А1D1/
и выполним построения на плоскости П4, типичные для способа замены
плоскостей проекций. Величина возвышения проекции D2 над
горизонтальной плоскостью проекций П1 равна /А1D1/
= /D1С1/ = /D1D4/.
Количество решений - два.
Задача 30. Обратим внимание, что АВ - горизонталь. На плоскости П4^АВ построим
двугранный угол с общим ребром [АВ], занимающим проецирующее
положение. Далее построим еще две плоскости проекций для определения истинной
формы граней АВС и АВD. В каждой из этих граней найдем точку,
равноудаленную от их вершин. Линии проекционных связей от этих двух точек однозначно
определят положение проекции О4 центра сферы на плоскости П4.
Проекцию О1 определим в точке пересечения линии проекционной
связи О4 О1 с перпендикуляром, проведенным
через середину [А1В1]. Остается установить
радиус искомой сферы, зная ее центр и точки на поверхности.
Задача 31. Строим три конические поверхности, касательные к сферам А и В, А и С, В и С.
Каждый из конусов коснется двух сфер по двум окружностям, занимающим горизонтально
проецирующее положение. В результате получим шесть таких окружностей, причем
по две на каждой сфере. Две окружности пересекаются в двух точках. Общее число
таких точек - 6. Три точки, расположенные
выше горизонтальной плоскости симметрии сфер, определят положение искомой плоскости,
касательной к трем сферам сверху. Это первое решение. Остальные три точки,
расположенные на нижних каждой из этих граней найдем точку, равноудаленную
от их вершин. Эти две точки однозначно определят положение проекции О4 центра
сферы на плоскости П4. Проекцию О1 определим
в точке пересечения линии проекционной связи О4 О1 с
перпендикуляром, проведенными через середину [А1В1].
Остается установить радиус искомой сферы, зная ее центр и точки на поверхности.
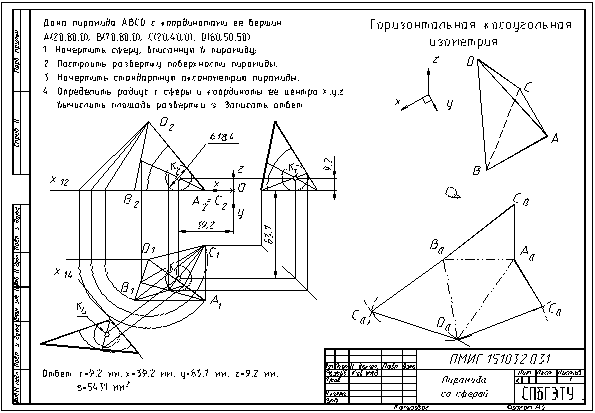
Задача 32. Центр сферы находится в точке пересечения трех биссекторных плоскостей,
построенных в произвольно взятых трех двугранных углах пирамиды. Проще всего
эти плоскости можно построить на фронтальной, профильной и дополнительной плоскостях
проекций. Последняя перпендикулярна к горизонтальной проекции горизонтали ВС.
В заключение приводим пример решения и оформления этой задачи, участвовавшей
в финале чемпионата С.-Петербурга в 2000 г. по инженерной компьютерной графике.
|